№1
это числа 8 и 6
№3
раскрываем скобки
а+1=0 х-2=0
а=-1 х=2
№2
1)0.50х/5/8=2х(чел)- мальчики
2)2х+х=36
3х=36
х=12(чел)-девочки
3)36-12=24(чел)-мальчики
ответ:12девочек, и 24 мальчика
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

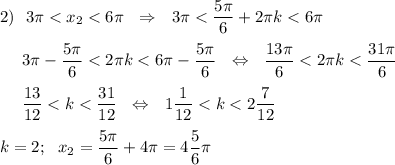
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 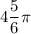
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

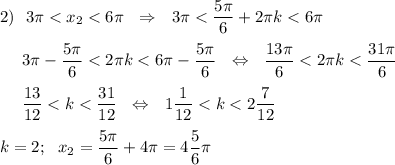
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 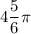
ЗАДАНИЕ 1
имеем систему уравнений
a+b=14
a-3*b=2
отнимем от первого уравнения второе
получим
a+b-(a-3*b)=14-2
a+b-a+3*b=12
4*b=12
ОТВЕТ№1:
a=11
b=3
ЗАДАНИЕ 2
мальчики- a, девочки -b
состьавим систему уравнений и решим её
a+b=36
5/8*a=1/2*b
тогда имеем
5a=4b
a=36-b
36*5-5b=4b
180=9b
b=180/9=20
a=16
можно это проверить, подставивши в стартовое уравнение
ОТВЕТ№2:
мальчиков 16
девочек 20
всё работает, ответ правильный
ЗАДАНИЕ 3
если a+1<0 либо a+1>0 то решение только при х=2
если же a+1=0
тогда при любых х, будет равенство выполняться, так как 0*(х-2)=0
ОТВЕТ№3: a=-1