Олимпийское движение постоянно совершенствуется, со временем
приобретая положительные тенденции своего развития. МОК (Международный
Олимпийский комитет) уделяет немало внимания проблемам Игр и по мере сил
старается их решить. Это, в частности, касается организации Юношеских
Олимпийских игр. Первые летние Игры начали проводить только с 2010 года, а
зимние – с 2012. Предшественниками юношеской Олимпиады стали всемирные
соревнования, в которых принимали участие спортсмены-юниоры, возраст
которых варьировал от 14 до 18 лет. Целью организации подобных
мероприятий стало стремление вовлечь молодежь в официальное Олимпийское
движение юниорам реализовать таланты, а также найти сильных
спортсменов, которые будут достойны представлять свои страны на
последующих Играх.
Прекрасным примером достойного участника юношеской Олимпиады
является Никита Владимирович Нагорный, российский гимнаст, рожденный 12 февраля 1997 года в Ростове-на-Дону. Никита в свои девятнадцать является
трехкратным чемпионом, серебряным и бронзовым призѐром юношеских
Олимпийских игр 2014 года, чемпионом Европы 2015 года в опорном прыжке,
чемпионом Европы 2016 в командном первенстве и в вольных упражнениях,
серебряным призѐром летних Олимпийских игр 2016 года. Он - заслуженный
мастер спорта России, а также мастер спорта международного класса, а ко
всему еще и младший лейтенант Вооруженных Сил Российской Федерации.
За высокие спортивные достижения, за волю к победе и
целеустремленность, Никите вручили медаль ордена «За заслуги перед Отечеством».
Другой положительной тенденцией развития Олимпийского движения в
лучшую сторону стало постепенное вовлечение в него женщин, а также
исправление гендерной асимметрии. Вплоть до 1981 года в МОК не входила ни
одна женщина, поскольку решение о составе Комитета принимали его
участники, т.е. мужчины.
Одним из примеров таких личностей является Ольга Геннадьевна
Вилухина, российская биатлонистка. Она занималась лыжными гонками до
1998 года, но с 2004 года перешла на биатлон по совету тренера. Чемпионат
мира по биатлону среди юниоров 2006 года стал для нее первым в карьере. В
индивидуальной гонке она заняла лишь 28 место.
На сегодняшний день Ольга является заслуженным мастером спорта
России, двукратным серебряным призером Олимпийских игр 2014 года (в
спринте и женской эстафете), бронзовым призером чемпионата мира 2012 года,
трехкратной чемпионкой России.
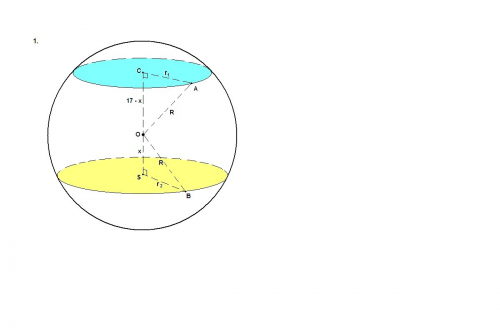
1. Сечение шара - круг. Площадь круга: S = πr².
S₁ = πr₁² = 25π ⇒ r₁ = 5
S₂ = πr₂² = 144π ⇒ r₂ = 12
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению.
Обозначим ОС = х, тогда OS = 17 - х.
Из прямоугольных треугольников ОСА и OSB выразим радиус шара по теореме Пифагора:
R² = (17 - x)² + r₁² = (17 - x)² + 25
R² = x² + r₂² = x² + 144
(17 - x)² + 25 = x² + 144
289 - 34x + x² + 25 = x² + 144
34x = 170
x = 5
R = √(x² + 144) = √(25 + 144) = √169 = 13
Sпов. шара = 4πR² = 4 · π · 169 = 676π
2. Так как вершины квадрата лежат на сфере, то квадрат вписан в сечение сферы, в окружность, центр которой лежит в точке пересечения диагоналей квадрата.
Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен сечению. Тогда SD - проекция наклонной OD на плоскость АВС, значит ∠SDO = 60° - угол между радиусом и плоскостью АВС.
OS - искомое расстояние.
BD = 12√2 как диагональ квадрата,
SD = 6√2.
Из прямоугольного треугольника SOD:
tg 60° = SO / SD
SO = SD · tg 60° = 6√2 · √3 = 6√6
3. Так как стороны треугольника касаются шара, то круг - сечение шара - вписан в треугольник.
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению.
OS = √2 - расстояние от центра шара до плоскости треугольника.
Полупериметр треугольника АВС:
p = (8 + 10 + 12)/2 = 15
По формуле Герона:
Sabc = √(p·(p - AB)·(p - BC)·(p - AC))
Sabc = √(15 · 7 · 5 · 3) = √(5 · 3 · 7 · 5 · 3) = 15√7
Sabc = p·r, где r = SK - радиус вписанной окружности.
p · SK = 15√7
SK = 15√7 / 15 = √7
Из прямоугольного треугольника SOK по теореме Пифагора:
ОК = √(SK² + OS²) = √(7 + 2) = √9 = 3
R = 3
4. Ядро - шар. Если его переплавили в конус, значит объем шара и конуса одинаков.
Пусть R = 1 - радиус шара, r - радиус конуса.
Vшара = 4/3 π R³ = 4/3π
Vконуса = 1/3 πr² · h = 4/3π, отсюда
r² · h = 4
Из прямоугольного треугольника, образованного высотой, радиусом основания и образующей конуса, по теореме Пифагора:
r² + h² = 6
Получили систему уравнений:
r² · h = 4
r² + h² = 6
r² = 6 - h²
(6 - h²) · h = 4 (2)
Решим второе:
6h - h³ = 4
h³ - 6h + 4 = 0
(h - 2)(h² + 2h - 2) = 0
h = 2
или
h² + 2h - 2 = 0
D/4 = 1 + 2 = 3
h = - 1 - √3 - не подходит по смыслу задачи, или
h = - 1 + √3 - не подходит по условию, так как высота не меньше 1.
ответ: h = 2
2)начинаются с цифры 5
Пошаговое объяснение: