Пошаговое объяснение: Моторная лодка за 3 ч движения против течения реки и 2,5 ч по течению проходит 98 км. Найдите собственную скорость лодки и скорость течения, если за 5 ч движения по течению она проходит на 36 км больше, чем за 4 ч против течения реки.
Пусть х км/ч-собственная скорость лодки, у км/ч -скорость течения реки, тогда (х-у) км/ч -скорость лодки против течения, (х+у) км/ч -скорость лодки по течению, тогда 3(х-у) км пкть против течения, 2,5(х+у) км -путь по течению реки, тогда составим уравнение:
3(х-у)+2,5(х+у)=98
5(х+у) км -расстояние по течению за 5 час
4(х-у) км -расстояние против течения за 4 часа , тогда
5(х+у)-4(х-у)=36
Получим систему двух уравнений:
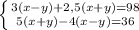
Упростим уравнения, раскрыв скобки:
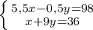
x=36-9y, ⇒ 5,5(36-9y) - 0,5y=98
198- 49.5y-0,5y=98
100= 50y
y=2(км/ч) -скорость течения реки,
х=36 - 9·2=18 (км/ч) - собственная скорость лодки
ДАНО
Y= (x²+1)/x.
ИССЛЕДОВАНИЕ
1. Область определения - Х≠0 - деление на 0.
Х∈(-∞,0]∪[0,+∞)
2. Пересечение с осью Х
Y(x) = 0 - Корней нет - нет точек пересечения.
3. Пересечение с осью Y
X∈ ∅
4. Поведение на бесконечности.
Y(-∞) = -∞
Y(+∞) = +∞
5. Наклонная асимптота
Y = x.
6. Исследование на четность.
Y(-x) = - (x²+1)/x
Y(x) = (x²+1)/x
Функция нечетная.
7. Производная функции
Y' = 2 - (x2+1)/x²
8. Корни производной.
Y' = 0. х1 = -1 и х2 = 1. - точки экстремумов.
9. Монотонность.
Возрастает - Х∈(-∞, -1]∪[1,+∞)
Максимум - Ymax(-1) = -2
Убывает- Х∈[-1,0]∪[0,1]
Минимум - Ymin(1) = 2.
10. Построение графика
в приложении.
Пошаговое объяснение:
так?

1.
1)13,6*9,4=127,84(м2)-S прямокутника
2)12*12=144(м2)-S квадрата
3)144-127,84=16,16(м2)
2.
1)205км:82км/год=2,5(год)-їхав спочатку
2)(471км-205км):76км/год=3,5(год)-решта
шляху
3)2,5+3,5=6 год
3.
180*0,6=108 сторінок
4.
1)10,2*6=61,2-коштує 6 кг бананів
2)(136,4-61,2):8=9,4-коштує 1 кг фіників