ответ:
пошаговое объяснение:
a1 = b1+2
a2 = b1*q+5
a3 = b1*q^2+7
a4 = b1*q^3+7
по свойствам арифметической прогрессии а1+а3=2а2
b1+2 + b1*q^2+7 = 2*b1*q+10
b1 - 2*b1*q + b1*q^2 = 10 - 7 - 2
b1*(1-2q+q^2) = 1
b1*(1-q)^2 = 1
b1 = 1/(1-q)^2
b1*g = q/(1-q)^2 [формула 1]
также по свойствам а2+а4=2*а3
b1*q+5 + b1*q^3+7 = 2*b1*q^2+14
b1*q - 2*b1*q^2 + b1*q^3 = 2
b1*q*(1-q)^2 = 2
b1*q = 2/(1-q)^2 [формула 2]
в формулах [1] и [2] левые части равны. приравниваем правые части
q/(1-q)^2 = 2/(1-q)^2
q = 2
b1 = 1/(1-q)^2 = 1/(1-2)^2 = 1
a1 = b1+2 = 1+2 = 3
a2 = b1*q+5 = 1*2+5 = 7
a3 = b1*q^2+7 = 1*2^2+7 = 11
a3 = b1*q^3+7 = 1*2^3+7 = 15
ответ: ответ №3
Пошаговое объяснение:
Вычислим в столбик первый и третий варианты ответа, получим соответственно 12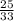
и 11
.
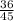Далее произведем оценку второго и четвертого вариантов:
2: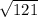 
< 
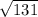, то есть данное число чуть больше 11 (т.к. 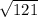= 11)
4: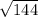 
< 
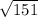, то есть данное число чуть больше 12 (т.к. 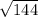= 12)
Точка А находится ближе к точке 11, визуально она соответствует числу, меньшему 12, а значит варианты 1 и 4 отпадают. Остается сравнить между собой 2 и 3 варианты:
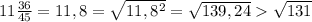
То есть третий вариант, численно равный 11,8, больше второго, и визуально ближе к середине отрезка.
1)40×100/25=160
2)2,5×100/25=10
3)170×100/25=680
4)62×100/25=248
5)100×100/25=400