
Длина изогнутой линии 420 см.
Объяснение:
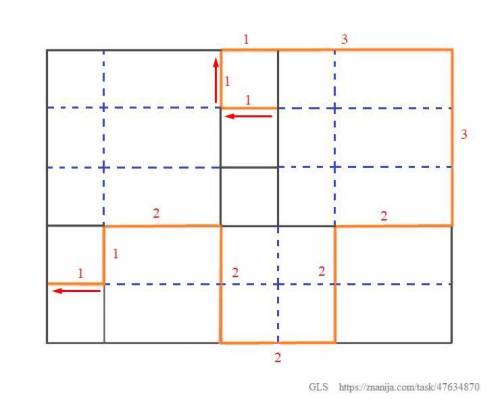
Найти длину отмеченной (оранжевой) линии на рисунке с изображением квадратов. Известно, что сторона меньшего квадрата 20 см.
Квадрат - это четырехугольник, у которого все стороны равны, все углы прямые.
1) Проведем на рисунке вс линии пунктиром, для того, чтобы оценить стороны всех квадратов (смотрим приложение).
2) Теперь мы видим, что
- сторона среднего квадрата равна двум сторонам наименьшего квадрата,
- сторона самого большого квадрата равна трем сторонам наименьшего квадрата.
3) Посчитаем, сколько раз длина стороны наименьшего квадрата входит в длину изогнутой линии.
Расставим количество длин маленького квадрата для каждого звена ломаной.
Посчитаем, сколько таких отрезков получилось.
Считать будем от верхнего малого квадрата по часовой стрелке и завершим подсчет на самом правом малом квадрате.
1 + 1 + 1 + 3 + 3 + 2 + 2 +2 +2 + 2 + 1 + 1 =
= 3 · 1 + 2 · 3 + 5 · 2 + 2 · 1 =
= 3 + 6 + 10 + 2 = 21.
4) Зная, что сторона малого квадрата равна 20 см, вычислим длину всей ломаной.
21 · 20 см = 420 см.
Длина изогнутой линии 420 см.
ответ: утверждение доказано.
Пошаговое объяснение:
Возьмём сколь угодно малое положительное число ε. Мы докажем утверждение, если найдём такое число N, что при n>N будет выполняться неравенство /(n+b)/n-1/<ε. Данное неравенство равносильно двойному неравенству -ε<(n+b)/n-1<ε, или 1-ε<(n+b)/n<1+ε. Решением неравенства 1-ε<(n+b)/n является n>-b/ε, решением неравенства (n+b)/n<1+ε является n>b/ε. И если взять большее из чисел -b/ε и b/ε (обозначим его через с), то в качестве числа N можно взять либо само число с (если оно натуральное), либо ближайшее к нему и меньшее его натуральное число. Тогда числа N+1, N+2будут заведомо удовлетворять неравенству. Таким образом, по числу ε найдено соответствующее ему число N, поэтому утверждение доказано.