41472
Пошаговое объяснение:
Пусть d - количество дней, c - количество деталей в день, b - количество заказчиков.
1 условие: "Когда треть продукции одного дня была упакована в ящики, то в каждом ящике оказалось столько деталей, сколько ящиков понадобилось для упаковки, причем число ящиков равно числу дней работы цеха. "
Треть продукции одного дня = c/3.
Число упакованных ящиков = числу деталей в ящике = числу дней работы цеха = d.
Получается, что упаковали d*d=d² деталей. Тогда c/3=d² или c=3d².
2 условие: "После отсылки половины всех деталей заказчикам выяснилось, что куб числа заказчиков был равен числу деталей, высланных каждому из заказчиков."
Половина всех деталей = cd/2
Куб числа заказчиков = b³
Число деталей, высланных каждому (в предположении, что оно одинаковое для каждого заказчика) = cd/2/b=cd/(2b).
Тогда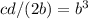 
или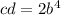 
.
Требуется найти минимальное положительное значение cd.
В выражение 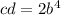вместо c подставим 3d². Тогда:
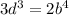
Требуется найти минимальное положительное решение этого уравнения. Заметим, что левая часть делится на 3, а правая на 2. Значит, каждая из частей должна делиться и на 2, и на 3. Тогда d и b можно представить в виде произведения степеней чисел 2 и 3 (другие множители нет смысла рассматривать, так как мы минимизируем ответ).
Пусть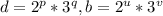 
.
Тогда левая часть равна:
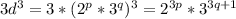
Правая часть равна:
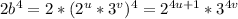
Согласно основной теореме арифметики, разложение числа на простые множители единственно. Поэтому можно приравнять соответствующие степени левой и правой частей равенства.
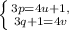
Легко подобрать минимальные подходящие решения:
p = 3, u = 2,
q = 1, v = 1.
Отсюда получим, что
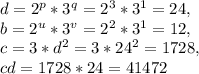
Пошаговое объяснение:
1. На 2 делятся все числа: В. оканчивающиеся чётной цифрой;
2. На 3 делятся все числа: Б: сумма цифр которых делится на 3;
3 На 5 делятся все числа: А: оканчивающиеся цифрами 0 и 5;
4 На 9 делятся все числа: В: сумма цифр которых делится на 9;
5 На 10 делятся все числа: Г:оканчивающиеся цифрой 0.
6 На 4 делятся все числа: Б: оканчивающиеся на две цифры, которые выражают число, которое делится на 4.;
7 Среди чисел 32 080; 1611; 3007; 91195; 1020930; 345140; 8816618 указать те, которые кратны 3: Б: 1611; 1020930;
8 Среди чисел 45678; 1300; 3456767; 7023; 40764 укажите те, которые не делятся на 2: А: 45678; 1300; 40764;
9 В школу привезли новые стулья. Мальчики перенести их в кабинеты, беря по 2 стула каждый раз. Сколько стульев могли привезти в школу? А: 108
10 Какие цифры можно подставить в число 761813* вместо *, чтобы полученное число делилось на 9? Б: 1; 10;
11 Мама купила для Васи канцелярские принадлежности. Весь товар продавец рассортировала в пакеты по 10 предметов в каждом. Может ли общее число предметов покупки быть равным? Б: 50;
12 Какие цифры можно подставить в число 601391* вместо *, чтобы полученное число делилось на 5? Б: 0; 5