63°
Пошаговое объяснение:
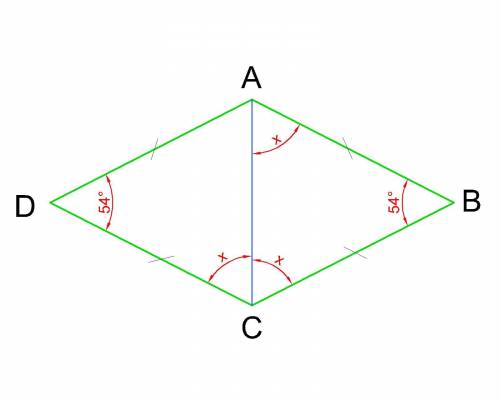
Выполним рисунок.
Вариант решения №1.
В ромбе противолежащие углы равны и сумма внутренних углов равна 360°. Диагонали ромба являются также и биссектрисами его углов.
Значит:
∠ACB=∠DCB/2=x
∠ADC=∠ABC=54°
∠DAB=∠DCB=2x
2*(∠ADC+∠DCB)=360° ⇒ 2(54°+2x)=360° ⇒ 4x=360°-108° ⇒ x = 63°.
Вариант решения №2.
В ромбе противолежащие углы равны и все стороны равны. Рассмотрим ΔАВС. Т.к. АВ=ВС, то он равнобедренный с углами при основании ∠САВ=∠АСВ=х. Тк. ∠ADC=∠ABC=54° и сумма внутренних углов треугольника равна 180°, то
Значит:
∠ACB+∠САВ+∠ABC=180°
2х+54°=180° ⇒ 2х=126° ⇒ x = 63°.
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
ответ: – 8.
Пример 3. Решите уравнение .
. Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
ответ: 3.
Пример 4. Решите систему
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
ответ: (1; 1).
Замечание. Если неизвестные системы х и у, то ответ можно записать в виде ко
Пошаговое объяснение:
надеюсь правильно