в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
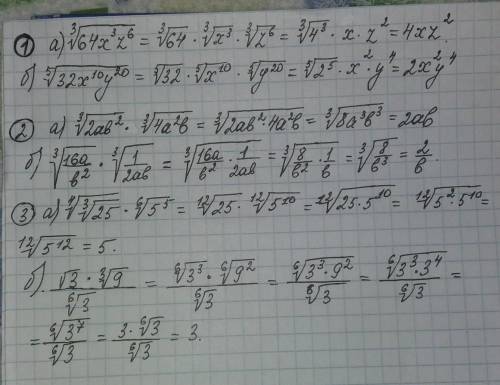
Следует разделить монеты на 3 кучки: 3 - 3 - 2
Первым взвешиванием двух частей по 3 монеты определяется часть, в которой есть фальшивая монета. Если части по 3 монеты уравновешены, то фальшивая монета в кучке на 2 монеты. Тогда вторым взвешиванием 2-х монет из третьей кучки определяют более легкую - она и будет фальшивой.
Если при первом взвешивании монеты имеют разный вес, то монета в более легкой кучке и тогда сравнивают 2 любые монеты из более легкой кучки. Если эти монеты уравновешены, то фальшивой является третья монета, а если имеют разный вес, то фальшивая монета - более легкая. Profit!
3√3 или ≈5,20
Пошаговое объяснение:
См рисунок.
Начнем с понятия "конус".
Конус - Геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов Рассмотрим прямоугольный Δ АОВ:
∠ВАО по условию =60°, можно найти ∠АВО=180°-60°-90°=30° ⇒
сторона, лежащая напротив угла 30° равна половине гипотенузы⇒
АО=6/2=3
АВ=6 (по условию)
Тогда, по теореме Пифагора ОВ² =h²=6²-3³=36-9⇒h=√27=√9*3=3√3
h=3√3≈5,19615....
Поверим (3√3)²+3²=27+9=36=6² - верно