Пошаговое объяснение:
№ 1. В новой квартире хотят поставить окно. Ширина окна должна быть 1 м 20 см, а длина 1 м узнать периметр окна и правильно его поставить.
1 м – 100 см
100 + 20 = 120 (см)
P = 2 × (100 + 120) = 2 × 220 = 440 (см)
ответ: P = 440 см.
№ 2.
В новой квартире так же хотят поставить дверь длиной 2 м 10 см и шириной 1 м. Теперь нужно узнать какова площадь двери.
2 м = 200 см
200 + 10 = 210 (см)
S = 210 × 100 = 21000 (см²)
ответ: S = 21000 см²
№ 3. Комната в новой квартире имеет высоту 2 м 80 см, ширину 5 м и длину 3 м. Узнайте объём данной комнаты.
2 м 80 см = 280 см
280 × 500 = 140000 см² = 1400 м²
1400 × 3 = 4200 м³
ответ: 4200 м³
1)
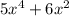
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
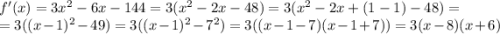
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
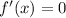
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
Пошаговое объяснение:
2/4 дм=5см
5см=50 мм