Ранжируем данный ряд (разместим элементы данного ряда в порядке возрастания):
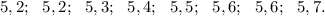
Размах выборки  — это разность между наибольшим и наименьшим значениями случайной величины в выборке:
— это разность между наибольшим и наименьшим значениями случайной величины в выборке:
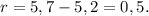
Среднее арифметическое 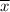 — сумма
— сумма 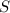 всех элементов выборки, поделенное на их количество
всех элементов выборки, поделенное на их количество 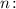
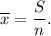
Сумма элементов выборки: 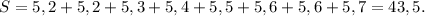
Количество элементов выборки: 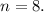
Среднее арифметическое выборки: 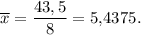
Мода 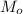 — это то значение случайной величины, которое встречается наиболее часто.
— это то значение случайной величины, которое встречается наиболее часто.
Имеем две моды: 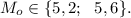
Медиана 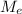 — это так называемое срединное значение упорядоченного ряда значений случайной величины:
— это так называемое срединное значение упорядоченного ряда значений случайной величины:
— если количество элементов в ряду нечетное, то медиана — это число, записанное посередине;
— если количество элементов в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
В нашем ряду количество элементов четное (8 элементов). Два срединных элемента выборки: 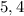 и
и 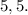
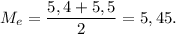
ответ: 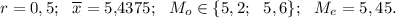
384 × 736 ÷ ( 2 745 - 2 721 ) - ( 5 560 - 1 060 ) ÷ 2 = 9 526
1) 2 745 - 2 721 = 24
2) 5 560 - 1 060 = 4 500
3) 384 × 736 = 282 624
4) 282 624 ÷ 24 = 11 776
5) 4 500 ÷ 2 = 2 250
6) 11 776 - 2 250 = 9 526
( 1 125 + 875 ) × 18 + 4 328 + ( 976 543 - 123 459 ) × 1 = 893 412
1) 1 125 + 875 = 2 000
2) 976 543 - 123 459 = 853 084
3) 2 000 × 18 = 36 000
4) 853 084 × 1 = 853 084
5) 36 000 + 4 328 = 40 328
6) 40 328 + 853 084 = 893 412
2 025 ÷ 15 × ( 524 + 195 ) ÷ 9 + ( 308 308 - 207 207 ) × 2 = 212 987
1) 524 + 195 = 719
2) 308 308 - 207 207 = 101 101
3) 2 025 ÷ 15 = 135
4) 135 × 719 = 97 065
5) 97 065 ÷ 9 = 10 785
6) 101 101 × 2 = 202 202
7) 10 785 + 202 202 = 212 987
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от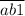 до
до  , либо от
, либо от  до
до  .
.
Значит, в любом случае среди этих чисел есть следующие:
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит
делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 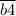 делится на 4,
делится на 4, 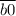 делится на 4,
делится на 4, 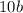 делится на 4,
делится на 4, 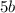 делится на 2, значит
делится на 2, значит  - четное.
- четное.
Рассмотрим утверждение ""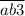 делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит,
делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 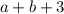 делится на 3,
делится на 3,  делится на 3. Выпишем пары цифр, где
делится на 3. Выпишем пары цифр, где  , а
, а  - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""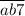 делится на 7"". Если
делится на 7"". Если 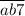 делится на 7, то
делится на 7, то 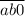 делится на 7,
делится на 7,  делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13