Пусть х руб. - стоимость фотоаппарата, тогда (5/8)х руб. было у первого брата, (4/7)х руб. было у другого брата, причём у первого было на 2,25 руб. больше. Уравнение:
(5/8)х - (4/7)х = 2,25
(35/56)х - (32/56)х = 225/100
(3/56)х = 9/4 (сократили на 25)
х = 9/4 : 3/56
х = 9/4 · 56/3 = (3·14)/(1·1)
х = 42 (руб.) - стоимость фотоаппарата
42 : 2 = 21 (руб.) - половина стоимости
5/8 · 42 = 42 : 8 · 5 = 26,25 (руб.) - было у первого брата
26,25 - 21 = 5,25 (руб.) - осталось у первого брата
4/7 · 42 = 42 : 7 · 4 = 24 (руб.) - было у второго брата
24 - 21 = 3 (руб.) - осталось у второго брата
ответ: 5,25 руб. осталось у первого и 3 руб. - у второго.
берем производную:
f(x)'=2(3x^2)-6=6x^2-6
ищем экстремиумы:
6x^2-6=0; x^2=1; x1=1; x2=-1
y1=0, y2=8;
у функции 2 экстремиума: (1;0) и (-1;8)
определяем методом интервалов возрастание/убывание:
возрастает: x=(-беск;-1] и [1;+беск)
убывает: x= [-1;1]
определаяем четность/нечетность:
f(-x)=2(-x)^3-6(-x)+4=-2x^3+6x+4=-(2x^3-6x-4) - функция не является ни четной ни нечетной;
ищем точки перегиба:
берем 2 производную:
f(x)''=6(2x)=12x
12x=0; x=0;
y=4; (0;4)
методом интервалов находим выпуклость/ вогнутсть:
выпукла: (-беск;0]
вогнута: [0;+беск)
собираем точки:
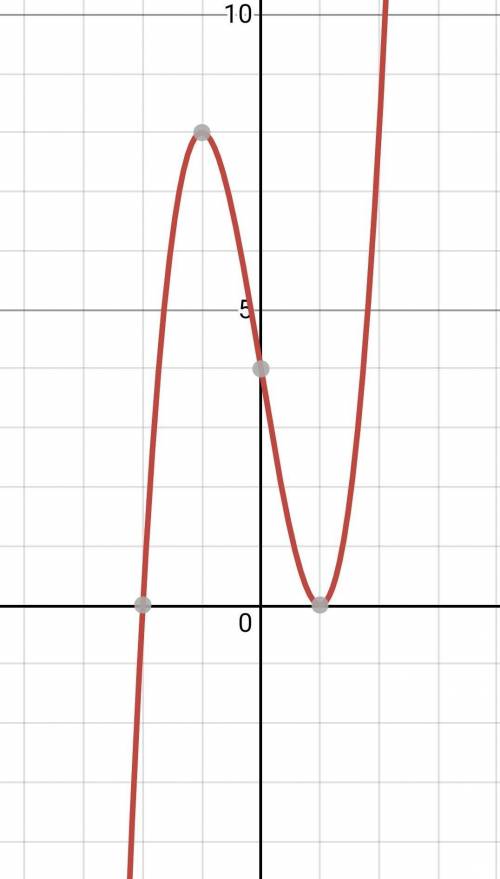
(1;0), (-1;8), (0,4)
и по ним строим график:
Чтобы число делилось на 18 необходимо, чтобы оно одновременно делилось на 9 и на 2.
Чтобы число делилось на 9, необходимо чтобы сумма его цифр делилась на 9. Так как 1+2+...+9=45, а 45 делится на 9, то и любое девятизначное число, составленное из этих цифр делится на 9.
Чтобы число делилось на 2, необходимо чтобы его последняя цифра делилась на 2. Всего на последнем месте может стоять любая из 9 цифр, но желательно, чтобы там стояла какая-либо из цифр 2, 4, 6, 8. То есть благоприятных событий - 4, общее число событий - 9.
Итак, число всегда делится на 9 и с вероятностью 4/9 делится на 2. Значит и на 18 оно будет делится с вероятностью 4/9.
ответ: 4/9