Боковая поверхность тела вращения S = 16,8π см².
Пошаговое объяснение:
Рисунок прилагается.
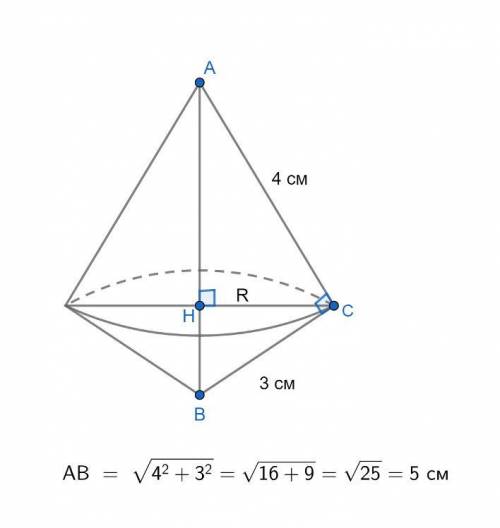
При вращении прямоугольного треугольника ABC вокруг прямой, содержащей гипотенузу AB получается тело вращения, образованной двумя конусами с общим основанием и образующими, равными катетам треугольника AC и BC. Радиус основания конусов R равен высоте CH треугольника ABC, проведенной из вершины прямого угла C.
В ΔABC ∠C = 90°, катет AC = 4 см, катет BC = 3 см. По т.Пифагора найдем гипотенузу AB:
AB =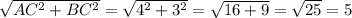 
(см).
Найдем высоту CH в ΔABC.
Воспользуемся определением синуса угла в прямоугольном треугольнике: синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
В ΔAHC: sin∠A =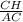 
;
В ΔABC: sin∠A =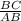 
;
; 
;
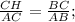
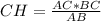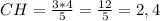Радиус основания конусов R = CH = 2,4 см.
Боковая поверхность конуса равна половине произведения длины окружности основания на образующую. S =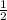 
* 2πR *L = πRL.
Боковая поверхность тела вращения равна сумме боковых поверхностей обоих конусов.
S₁ = π * 2,4 см * 4 см = 9,6π см²;
S₂ = π * 2,4 см * 3 см = 7,2π см²;
S = S₁ + S₂ = 16,8π см².
2 1/7 + 1 1/3 = 2*7+1/7 + 1*3+1/3 = 15/7 + 4/3 =45/21 + 28/21 = 45+28 /21 = 73/21 =3 10/21