1. Область определения - Х∈(-∞;+∞) - непрерывная
2. Пересечение с осью Х. Y=0 при х₁ = 2/3, х₂ = 1.
3. Пересечение с осью У. У(0) = 2.
4.Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) = 3x²+5x+2 ≠ Y(x).
Функция ни чётная ни нечетная.
6. Производная функции.Y'(x)= 6*x +5.
7. Корень при х = 5/6 ≈ 0,83.
Минимум – Ymin=(5/6) = - 1/12 ≈ - 0,0833.
Возрастает - Х∈(5/6;+∞). Убывает = .Х∈(-∞;5/6)
8. Вторая производная - Y"(x) = 3
9. Точек перегиба - нет.,
Вогнутая – «ложка» Х∈(-∞;+∞)
10. График в приложении. Функция и производная.
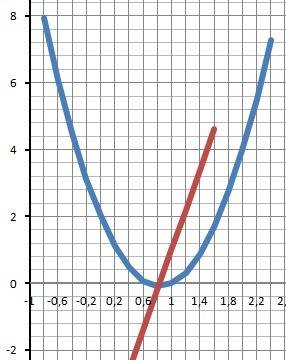
Похожа задача
Приклад 2.6У шухляді 12 деталей, з яких п’ять пофарбовані. Збирач випадково взяв три деталі. Знайти імовірність того, що хоча б одна з деталей буде пофарбована.
Розв’язання. Позначимо подія А – хоча б одна із трьох деталей пофарбована. Тоді – жодна з трьох деталей не пофарбована. Оскільки протилежна подія складається тільки з одного варіанту, то знайдемо її ймовірність, використовуючи класичне визначення ймовірності, тобто , , де сім – число нефарбованих деталей. Звідки за формулою (1.5) одержимо: . Тепер за формулою (2.8) одержимо шукану ймовірність .
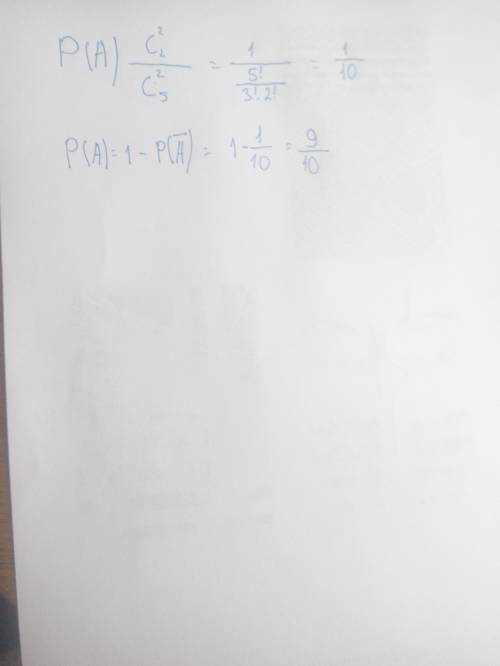
5,3
Пошаговое объяснение:
1) 2 2/3 - 1/6 = 2 4/6 - 1/6 = 2 1/2
2) 3,8 - 4,2 = -0,4
3) 2,4 + 2 1/2 = 2,4 + 2,5 = 4,9
4) 4,9 -(-0,4) = 4,9 + 0,4 = 5,3