Прямоугольный треугольник, гипотенуза которого равна 25, а один из катетов равен 15, вращается вокруг большего катета. Найдите площадь полной поверхности тела вращения.
Изучаемый прямоугольный треугольник имеет катеты и и гипотенузу (чертеж в приложении).
При этом, третья сторона была вычислена по теореме Пифагора: .
Из этого следует, что вращали треугольник вокруг катета, равного (это есть больший катет, ).
При вращении прямоугольного треугольника вокруг одного из катетов, как известно, получается конус. В данном случае его высота равна , радиус основания и образующая .
Для вычисления полной поверхности конуса используем соответствующую формулу:
Это одно из свойств алгоритмов: Дискретность – процесс решения задачи должен быть разбит на последовательность отдельных шагов. Понятность. Алгоритм должен быть понятен исполнителю и исполнитель должен быть в состоянии выполнить его команды. Определенность. Алгоритм не должен содержать команды, смысл которой может восприниматься неоднозначно. Результативность. Процесс решения задачи должен прекратиться за конечное число шагов и при этом должен быть получен ответ задачи. Массовость. По одному алгоритму можно решать однотипные задачи
Задача на движение Дано: v₁=250 м/мин. v₂=200 м/мин. S= 4 км 500 м tвстр.=? мин. Решение 1) v(сближ.) = v₁+v₂=250+200=450 (м/мин.) - скорость сближения двух лодок. 2) 1 км = 1000 м 4 км 500 м = 4*1000 м + 500 м =4500 м tвстр.=4500:450=10 (мин.) - нужно двум лодкам, чтобы встретиться. ОТВЕТ: 10 минут.
ОБРАТНАЯ ЗАДАЧА. От берегов протоки, ширина которой составляет 4 км 500 м, навстречу друг другу одновременно поплыли 2 лодки. Через 10 минут они встретились. Найдите скорость второй лодки, если скорость первой лодки 250 м/мин. 4500:10-250 (=200 м/мин. - скорость второй лодки)
Изучаемый прямоугольный треугольник имеет катеты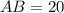 и
и 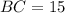 и гипотенузу
и гипотенузу 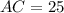 (чертеж в приложении).
(чертеж в приложении).
При этом, третья сторона была вычислена по теореме Пифагора:Из этого следует, что вращали треугольник вокруг катета, равного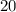 (это есть больший катет,
(это есть больший катет, 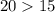 ).
).
При вращении прямоугольного треугольника вокруг одного из катетов, как известно, получается конус. В данном случае его высота равна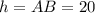 , радиус основания
, радиус основания 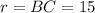 и образующая
и образующая 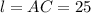 .
.
Для вычисления полной поверхности конуса используем соответствующую формулу:
Подставляем известные значения:
ответ: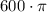 или около
или около 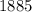 (ед³).
(ед³).