ответ: Увеличение на: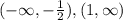 
Убывает на: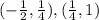 
.
Пошаговое объяснение: Найдем производную.
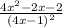
Приравняем производную к 0.
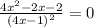
Решим относительно x.
Упростим числитель.
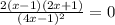
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
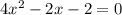
Решим уравнение.
Разлагаем на множители левую часть уравнения.
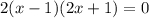
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
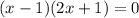
Приравняем x-1 к 0, затем решим относительно x.
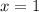
Приравняем 2x+1 к 0, затем решим относительно x.
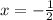
Решение является результатом x-1=0 и 2x+1=0.
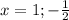
Значения, которые обращают производную в 0 - 1, 
.
1, .
Выясним, при каких значениях переменной функция 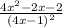не определена.
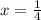
Разобьем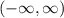 
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
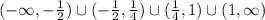
Подставим значение из интервала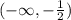 
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на 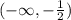, так как 
.
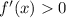Подставим значение из интервала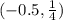 
в производную, чтобы определить, возрастает или убывает функция.
Убывает на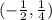 
, поскольку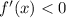 
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на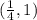 
, поскольку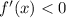
Подставим значения из интервала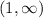 
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на 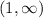, так как .
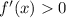Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: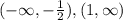
Убывает на: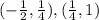
{x-3y=4
{x²-2xy-y²=2.
{х=4+3у
{х²-2ху-у²=2
(4+3у) ²-2(4+3у) у-у²=2
у=-7
у=-1
х= 4+3 (-7)
х= 4+3 (-1)
х=-17
х=1
(х1, у1) = (-17, -7)
(х2, у2) = (1, -1)
{-17-3(-7) = 4
{(-17) ²-2 (-17) (-7) - (-7) ² =2
{1-3(-1) =4
{1²-2•1(-1) - (-1) ²=2
(х1, у1) = (-17, -7)
(х2, у2) = (1, -1)