В группе спортсменов занимаются 50 велосепидистов Количество гимнастов составляют 32% количество всех велосепидистов 4/7 количество лыжнеков посещающех эту группу.Сколько гимнастов и лыжнеков посещают эту группу ?
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: ; В следующих двух слагаемых вынесем общий множитель "40": ; В итоге получим следующее уравнение: . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо будет стоять ; Это приведет к тому, что придется убавить ; В итоге: ; Слева стоит квадрат суммы. Уравнение примет вид: ; Сворачивая еще раз: ; Получаем серию прямых: ; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом ; Рассмотрим прямую ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты ; Ну а все решения:
Социальное прогнозирование – некоторое вероятностное знание о будущем состоянии общества и отдельных его сторон. В отличие от умозрительных представлений основывается на определенных познавательных процедурах. Их три: экстраполяция – мысленное прослеживание в будущем тенденций без каких-либо изменений; моделирование – построение некоторых будущих состояний общества, исходя из каких-либо теоретических предложений о их изменении; сценарий будущего – при прогнозировании соц. отношений и действий. Социальный прогноз – вид знаний, специфичный по функциям, поскольку во многих случаях его целью является знание о будущем, которое не наступит, или хотелось, чтоб не наступило. И в этом случае корректирование человеческой деятельности должно носить вероятностный, ориентировочный характер. В развитии общества планирование является гибким процессом. Соц. прогнозирование вероятностно в двойном смысле – поскольку само социальное развитие многовариантно, постольку любой прогноз описывает одну из возможных состояний системы (не всегда самое вероятное). Само знание, воплощенное в прогноз, является вероятностным по своей природе. Особенности: 1. формулировка цели носит сравнительно общий и абстрактный характер: она допускает большую степень вероятности. Цель соц. прогнозирования – на основе анализа состояния и поведения системы в и изучения возможных тенденций изменения факторов, влияющих на рассматриваемую систему, правильно определить вероятностные количественные и качественные параметры ее развития в перспективе, раскрыть варианты ситуации, в которой окажется система. 2. Соц. прогнозирование не обладает директивным характером. Др. словами, качественное отличие вариантного прогноза от конкретного плана заключается в том, что прогноз дает информацию для обоснования решения и выбора методов планирования. Он указывает на возможность того или иного пути развития в будущем, а в плане выражено решение о том, какую из возможностей общество реализует. 3. Соц. прогнозирование обладает специфическими методами:сложная проведения эксперимента.
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: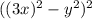 ; В следующих двух слагаемых вынесем общий множитель "40":
; В следующих двух слагаемых вынесем общий множитель "40":  ; В итоге получим следующее уравнение:
; В итоге получим следующее уравнение: 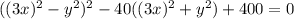 . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо
. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо  будет стоять
будет стоять  ; Это приведет к тому, что придется убавить
; Это приведет к тому, что придется убавить 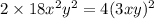 ; В итоге:
; В итоге: 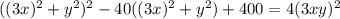 ; Слева стоит квадрат суммы. Уравнение примет вид:
; Слева стоит квадрат суммы. Уравнение примет вид:  ; Сворачивая еще раз:
; Сворачивая еще раз: 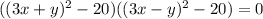 ; Получаем серию прямых:
; Получаем серию прямых:  ; А теперь приступим к рассмотрению первого уравнения.
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом ; Рассмотрим прямую
; Рассмотрим прямую 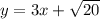 ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников.
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 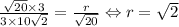 ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты
; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 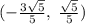 ; Ну а все решения:
; Ну а все решения: