168(м³) заготовила бригада за 7 дней
Пошаговое объяснение:
Количество заготовленной древесины по дням - это арифметическая прогрессия.
Пусть в 1-й день заготовили древесины а₁ (м³), тогда во второй а₂=а₁+d (м³) и т.д. в n-й а₁+d*(n-1) (м³)
В 5-й день заготовили: а₅=а₁+4d(м³) , в 6-й день:а₆=а₁+5d(м³).
Сложим количество древесины за 1,5 и 6-й дни:
а₁+а₁+4d+а₁+5d=72
3а₁+9d=72, разделим на 3
а₁+3d=24
За 7 первых дней заготовили: S₇=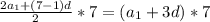 (сумма семи первых членов арифметической прогрессии).
(сумма семи первых членов арифметической прогрессии).
а₁+3d=24 подставим в S₇ и получим S₇=24*7
S₇=168(м³) - заготовила бригада за 7 дней
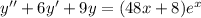
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
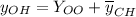
Решим однородное дифференциальное уравнение, соответствующее данному неоднородному:
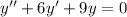
Составим и решим характеристическое уравнение:
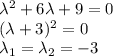
Запишем общее решение однородного уравнения:
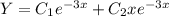
Частное решение будем искать в виде:
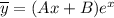
Найдем первую и вторую производную:
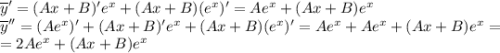
Подставим значения функции и первых двух производных в исходное уравнение:
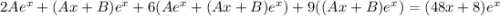
Сократим на 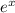 :
:
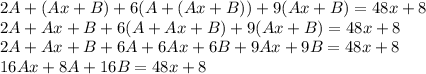
Так как левая и правая часть равны, то коэффициенты при х и свободные члены также равны. Получаем систему:
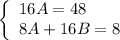
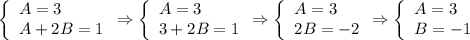
Тогда частное решение имеет вид:
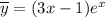
Общее решение заданного уравнения:
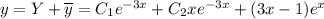
ответ: 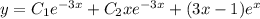
Запишем область определения:
Оба логарифма по основанию 3, поэтому значки логарифмов мы можем откинуть:
1-х < х+3
1-3 < х+х
-2 < 2х
х > -1.
Чертим числовые оси для всех неравенств (в том числе и для неравенств из области определения), находим промежуток, который совпадает на всех числовых осях, и записываем ответ.
ответ: ( -1;1)