Для того, чтобы находить и точки экстремума, и наибольшее с наименьшим необходимо работать с проихводной и с подстановкой значений крайних точек отрезка.
Ищем производную:
1) y' = 12/cos^2(x) - 12. Приравниваем ее к нулю для нахождения точек экстремума. (часто именно точки максимума и минимума могут быть наим и наиб значениями функции):
12/cos^2(x) - 12=0;
12/cos^2(x)=12;
cos^2(x)=1; (по правилу пропорции определить лёгко)
сosx = 1 или cosx=-1
x = 0 x = Пи
далее определям через занки производной возростание и убывание функции, по итогаам сих рассуждений получим: Пи - точка минимума. (значит, не подходит), а 0 - просто точка, через нее функция ни возрастает, ни убывает
2) находим значения функции на концах отрезка [-пи/4; пи/4]:
а) y(-Пи/4)= 12tg(-Пи/4) - 12(-Пи/4) + 3Пи - 13 = 12 + 6Пи - 13 = -1 (я не учел 6Пи - это оборот целый, он ничего не значит в данном случае и им можно пренебречь)
б) y(Пи/4) = 12tg(Пи/4) - 12(Пи/4) + 3Пи - 13 = 12 - 6Пи + 3Пи - 13 = -Пи - 1 = -4,14 (приближенно)
Итог: у нас есть точки -4,14 и - 1. большая из них -1. Это и есть ответ.
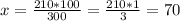
ответ: Границы участка: 60 м, 80 м, 100 м.
Пошаговое объяснение:
1 Га = 10000 м2, следовательно площадь участка равна 2400 м2.
Пусть х (м) – один катет, второй: х+20 (м)
Площадь треугольника равна
1/2 * х * (х+20) = 2400
х2 + 20 х = 2400 *2
х2 + 20 х – 4800 = 0
х1 = 60; х2 = -80 (не удовлетворяет условию)
Следовательно, один катет равен 60 м,
второй 60 + 20 = 80 м,
гипотенуза 2√(602 + 802) = 100 м.