Лунное затмение бывает в полнолуние, когда оппозиция Солнца и Луны происходит вблизи лунных узлов. Сам аспект оппозиции считается напряженным, а потому любое полнолуние связывают со всплесками эмоций и повышенной нервозностью.
Лунные затмения вызывают еще большее беспокойство, неуравновешенность и повышенную эмоциональную возбудимость, что может спровоцировать на конфликты, истерики и неуместный энтузиазм. В это время чаще всего случаются бурные выяснения отношений, скандалы, особенно на почве ревности. Возможна бессонница, лунатизм и иные нарушения сна. Многих в это время беспокоят головные боли, отеки, чаще происходят отравления, поскольку желудок человека становится чувствительнее, а влияние лекарств, алкоголя и ядовитых веществ в это время усиливается. Затмение Луны больше влияет на женщин и детей.
Солнечные затменияСолнечные затмения происходят в новолуние, когда соединение Солнца и Луны происходит вблизи одного из узлов Луны. Соединение светил совпадает с так называемыми днями Гекаты — богини ночного мрака, когда жизненная энергия на минимуме, сопротивляемость болезням слаба. Повышается риск инфарктов и инсультов. Во время солнечного затмения обычно чувствуется слабость, подавленность, ощущение бессилия как физического, так умственного. В эти дни не хочется предпринимать никаких активных действий,человеком овладевает уныние или безволие, подверженность влиянию извне. Тяжелее переживают солнечные затмения мужчины, а также руководители и творческие личности обоего пола.
Полное решение в прикрепленном файле, здесь некоторые подробные расчеты пропущены, так как слишком длинное решение не хочет добавляться.
Продифференцируем первое уравнение:
Подставим выражение для y' из второго уравнения:
От получившегося уравнения отнимем первое уравнение системы:
Решим однородное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение:
Предположим, что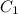 и
и 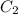 не константы, а некоторые функции
не константы, а некоторые функции 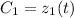 и
и 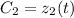 .
.
Найдем первую производную:
Пусть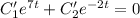 . Тогда:
. Тогда:
Найдем вторую производную:
Подставим значения функции и производных в уравнение относительно х:
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
Из первого уравнения выразим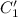 :
:
Подставим во второе уравнение:
Найдем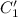 :
:
Необходимо проинтегрировать выражения для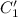 и
и 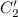 . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
. Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
1)
2)
3)
4)
Интегрируем выражение для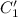 :
:
Интегрируем выражение для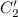 :
:
Подставляем выражения для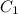 и
и 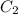 в решение:
в решение:
Найдем производную:
Из первого уравнения исходной системы выразим у:
Подставляем выражения для х и х':
ответ: