Пусть векторный случайный процесс на входе системы описывается параметрами mx , ∑х, а помеха ξ описывается параметрами m ξ , ∑ ξ . Найдите условия сходимости алгоритма Качмажа в случаях: 1 когда компоненты входного сигнала независимы между собой; 2 когда компоненты входного сигнала статистически зависимы и распределены по равномерному закону. 3 Найдите условия робастной устойчивости системы управления. Замечания. Помеха и ξ и входной сигнал статистически не зависимы.Пусть векторный случайный процесс на входе системы описывается параметрами
mx , ∑х, а помеха ξ описывается параметрами m ξ , ∑ ξ . Найдите условия сходимости
алгоритма Качмажа в случаях: 1 когда компоненты входного сигнала независимы между
собой; 2 когда компоненты входного сигнала статистически зависимы и распределены по
равномерному закону. 3 Найдите условия робастной устойчивости системы управления.
Замечания. Помеха и ξ и входной сигнал статистически не зависимы.
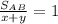 час
час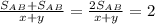 часа.
часа.
Можно написать через формулу:
Пусть х-скорость первого велосипедиста, а у- скорость второго велосипедиста, тогда
Поскольку каждый велосипедист проехал расстояние от А до B, тогда каждый из них проехал S, а значит на все расстояние от A до В было затрачено
После этого у них была стоянка 2 часа, и они выехали обратно, время до встречи нам уже известно 1 час, значит
2+2+1=5 часов времени они потратили до второй встречи
ответ 5 часов