На пришкільній ділянці 3 класи посадили 400 дерев. 1-А клас посадив 35% усіх дерев, а 5-Б на 52 дерева більше ніж 5-В клас. Скільки дерев посадив кожен клас?

👇

Увидеть ответ

Ответ:

Dima1234567y

13.10.2021

1-А- 140 дерев, 5-Б- 156 дерев, 5-В- 104 дерева.

Пошаговое объяснение:

Нехай 5-В посадив - х дерев, тоді 5-Б - (х + 52) , а 1-А - 0,35*400= 140. Складемо рівняння:

Х+ (х+52)+140= 400

2х+52+140= 400

2х= 400-52-140

2х= 208

Х= 104 дерев- посадив 5-В

104+52= 156 дерев - посадив 5-Б

4,5(68 оценок)

Ответ:

margarita030620

13.10.2021

Дивись

Надіюсь правильно :)

400 усе

35% від 400 140 дерев посадив 1-а

одже лишається 65 % тобто 260

на 52 дерева посадив 5-б більше значить від 260 - 52 = 208

далі 208 : 2 = 104

одже 104 + 52 = 156 ( д. ) посадив 5-б клас

Відповідь: 1-а посадив 140 дерев, 5 - в посадив 104 і 5-б посадив 156 дерев

4,7(39 оценок)

Открыть все ответы

Ответ:

Kotik77789

13.10.2021

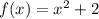Пусть функция f(x)=x^2+2

определена на множестве E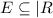 $E\subseteq |R$
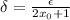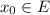Пусть $\delta=\frac{\epsilon}{2x_0+1}$ где $x_0 \in E$ .
Понятно, что для любого

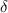на области $\delta$ от x_0

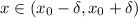(то есть: $x \in 
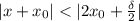(x_0-\delta,x_0+\delta)$ ) выполняется $|x+x_0|<|2x_0+ \frac{\delta}{2}|$ .
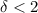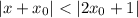Следовательно, для $\delta<2$ , выполняется |x+x_0|<|2x_0+1|

.

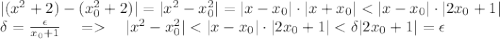
$|(x^2+2)-(x_0^2+2)|=|x^2-x_0^2|=|x-x_0|\cdot|x+x_0| < |x-x_0|\cdot|2x_0+1| \\
\delta= \frac{\epsilon}{x_0+1} \ \ \ = \ \ \ |x^2-x_0^2|< |x-x_0|\cdot|2x_0+1|<\delta|2x_0+1|=\epsilon$

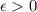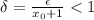Получили, что для любого $\epsilon 0$ есть $\delta=\frac{\epsilon}{x_0+1}<1$ , на области которой выполняется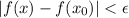 $|f(x)-f(x_0)|<\epsilon$
(Проще говоря:
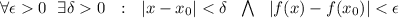$\forall
 \epsilon0 \ \ \exists\delta0 \ \ : \ \ |x-x_0|<\delta \ \ 
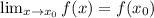\bigwedge \ \ |f(x)-f(x_0)|<\epsilon$ ). Следовательно - $\lim_{x 
\to x_0} f(x)=f(x_0)$ .
Что и требовалось доказать.
Для x_0=-1

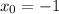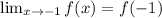нужно отдельно доказать предел $\lim_{x \to -1} f(x)=f(-1)$ .

Теперь в чём проблема самого вопроса: мы только что доказали непрерывность функции на любом подмножестве

. Но! Множество натуральных чисел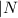

тоже подмножество

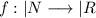, значит $f:|N \longrightarrow |R$ тоже непрерывна, получается - доказали что

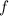непрерывна на области определения? Известно, что 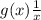$g(x) \frac{1}{x}$ тоже непрерывна на области определения, но

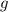, понятное дело, не определена на

!
Потому вопрос, ИМХО, поставлен не верно (претензия не к тебе, а скорее к преподавателям твоим). Правильно задать вопрос указывая то множесто точек, которое интересует: к примеру "непрерывна на

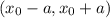" или, "непрерывна на отрезке (x_0-a,x_0+a)

"...
Тем более, что есть понятие "равномерная непрерывность" - свойство области, а не так, как "непрерывность" - свойство точки. Отсюда и непонимание.
А то получается: спрашивают об области, а проверяют точку.
Будут вопросы - пиши.

P.S. Исправил ошибки в наборе символов. Текста много :)

4,7(52 оценок)

Ответ: