1 5 + 99.4 = 1 5 + 99 4 10 = 99 + 1 5 + 4 10 = 99 + 1 · 2 5 · 2 + 4 · 1 10 · 1 = 99 + 2 10 + 4 10 = 99 + 2 + 4 10 = 99 + 6 10 = 99 + 3 · 2 5 · 2 = 99 + 3 5 = 99 3 5 = 99.6
99 3 5 + 7.3 = 99 3 5 + 7 3 10 = 106 + 3 5 + 3 10 = 106 + 3 · 2 5 · 2 + 3 · 1 10 · 1 = 106 + 6 10 + 3 10 = 106 + 6 + 3 10 = 106 + 9 10 = 106 9 10 = 106.9
106 9 10 - (-25.69) = 106 9 10 + 25.69 = 106 9 10 + 25 69 100 = 131 + 9 10 + 69 100 = 131 + 9 · 10 10 · 10 + 69 · 1 100 · 1 = 131 + 90 100 + 69 100 = 131 + 90 + 69 100 = 131 + 159 100 = 131 + 1·100 + 59 100 = 132 59 100 = 132.59
132 59 100 + 3.548 = 132 59 100 + 3 548 1000 = 135 + 59 100 + 548 1000 = 135 + 59 · 10 100 · 10 + 548 · 1 1000 · 1 = 135 + 590 1000 + 548 1000 = 135 + 590 + 548 1000 = 135 + 1138 1000 = 135 + 569 · 2 500 · 2 = 135 + 569 500 = 135 + 1·500 + 69 500 = 136 69 500 = 136.138
Если точки были отмечены на числовой прямой, то расположение точек зависит от нахождения координаты буквы С
Значит если С > В, то это прямая АВС
Если В>С>А, то АСВ,
Если С<А, то САВ
Координату точки первого варианта можно найти, поскольку точка С симметрична относительно точки В
В(24)-А(6)=С(х)-В(24)
С(х) =42
Поскольку АС=2ВС, значит, что АВ=ВС.
Координату точки второго случая, можно найти используя формулу из условия
АС=х-6
ВС=2*(24-х)
Отсюда х равен:
х-6=48-2х
х=18
Координату точки последнего случая найти невозможно, поскольку отрезок ВС больше отрезка АС, а значит равенство Условия не выполняется,
К примеру, если ВС=6, то АС=12, но поскольку С находится слева, то ВС>АС, но это не так...
Значит: сумма возможных х равна 18+42=60
ответ:60
a)
b)
Тут явно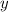 не выразить.
не выразить.