Пошаговое объяснение:
Пусть x% - концентрация раствора в первом сосуде, а y% - концентрация раствора во втором сосуде. Так как первый сосуд содержит 50 кг, а второй — 30 кг растворов кислоты, то суммарная масса кислоты в обоих сосудах, равна 50х+30у
. В задаче указано, что если растворы смешать, то получится раствор, содержащий 55% кислоты, то есть массу кислоты в них можно выразить 0,55(50+30)=0,55*80 .
Получаем уравнение:
50х+30у=0,55*80
50х+30у= 44
Второе уравнение получается из второго условия: если смешать равные массы этих растворов 1*х+1*у , то получится раствор, содержащий 60 % кислоты 0,6(1+1)=0,6*2 . Имеем уравнение:
х+у=0,6*2
х+у=1,2
Получаем систему уравнений:
50х+30у=44
х+у=1,2
умножим второе уравнение на -30
-30х-30у=-36
И схожим с первым уравнением
20х=8
х=8:20
х=0,4
то есть имеем в первом сосуде раствор 40% концентрации
значит масса кислоты будет
0,4*50= 20 кг
Пошаговое объяснение:
1) ООФ
здесь знаменатель всегда ≠ 0, поэтому ООФ - вся числовая ось
2) функция не тригонометрическая
3) пересечение с осью оу (х = 0)
у(0) = 0 точка (0;0)
с осью ох (у=0)
из дроби приравниваем к 0 числитель
5х² -30х = 5х(х -6) ⇒
х₁ = 0 точка (0;0)
х₂ = 6 точка (6;0)
4) критические точки
для нахождения производной используем
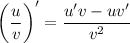
тогда
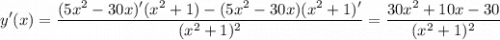
y'(x) = 0
10(3x² +x-3) = 0 ⇒ (значения определяем с точностью до 0,01)
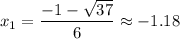
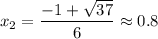
y(x₁) ≈ 17.707 точка (-1,18; 17,7)
у(х₂) ≈ -12,7 точка (0,8; -12,7)
5) промежутки возрастания и убывания. экстремумы
локальные экстремумы
у(≈-1,18) ≈ 17,7 - локальный максимум
у(≈0,8) ≈ -12,7 - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
6)
6) поскольку промежуток ООФ, то концы промежутка (-∞; +∞)
при х → -∞ f(x) f(x) → -∞
при х → +∞ f(x) f(x) → +∞
7)
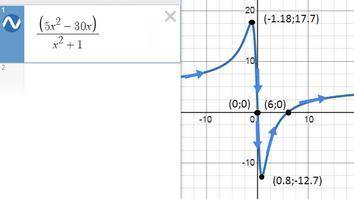
точки (0;0) (6;0)
(-1,18; 17,7) - локальный максимум
(0,8; -12,7) - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
график прилагается
Давным – давно была страна «Математика», в ней обитали цифры и знаки действия. И было там не много домов, а территории много. И вот стало одним жителям тесно в доме из ста чисел. Как вы понимаете, это были проценты. И пошли они к «Главной» задаче с :
- Дайте нам место для дома, так как стало очень тесно.
Главная задача ответила:
- Дам, если сможете решить задачу!
Заинтересовались проценты, а «Главная задача», говорит:
- Задам две задачи. Какое число будет в ответе, то и будет жить со мной.
Первая задача: «В магазин привезли 1200 пустых коробок для упаковки товара. Использовали только 300 коробок. Выяснить, сколько процентов составляют использованные коробки.»
Проценты хором закричали:
- 25%
- Иди сюда, двадцать пять сотых, - говорит «Главная» задача.
- Послушайте вторую задачу. Во время распродажи цена вазы, которая стоила 3000 рублей, была снижена на 600 рублей. На сколько процентов была снижена цена вазы?
- На 20 процентов.- ответили жители.
- Иди сюда, двадцать сотых!
Так 25% и 20% остались жить в доме «Главной » задачи, а остальные жители пошли дома строить. Со временем построив дома, стали они жить поживать, да добра наживать.
Пошаговое объяснение:
х-концентрация первого раствора (в долях от 1)
у - второго
тогда масса кислоты в 1 растворе 50х
масса кислоты во втором растворе 30у
50х+30у=44 - первое уравнение
если смешать равные массы (пусть по 30г), тогда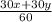 =0,6
=0,6
30х+30у=36
получилась система уравнений
выразим у из второго
30у=36-30х
у=1,2-х
подставим в 1 уравнение
50х+30(1,2-х)=44
50х+36-30х=44
20х=8
х=0,4
50*0,4=20кг кислоты в первом растворе