840 см²
Пошаговое объяснение:
S=h•a
∆ АВD равнобедренный. Высота ВН - его медиана.
АН=DH=21, т.е. мы 42:2=21
Высота по т.Пифагора
ВН=√(АВ²-АН²)=√(29²-21)=20
S=20•42=840 см²
2) Для определения площади параллелограмма можно применить следующие формулы:
а) Умножения высоты и стороны: S=h•a
b) Формулу Герона S=√p(p-a)(p-b)(p-c) для половины параллелограмма и последующего умножения на 2.
c) Формулу умножения сторон и синуса угла между ними: S=a•b•sinα=a•b•sinβ
d) Формула площади параллелограмма через диагонали и угол между ними:
S=0,5•D•d•sinα=0,5•D•d•sinβ
6 см, 8 см и 10 см.
Пошаговое объяснение:
Пусть один катет будет х см. Тогда второй катет (х+2) см. Периметр треугольника это сумма длин всех сторон. Тогда найдем гипотенузу прямоугольного треугольника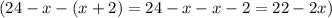 см. Составим уравнение на основании теоремы Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
см. Составим уравнение на основании теоремы Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Значит, один катет будет 6 см, второй катет 6+2=8см, а гипотенуза 24-(6+8)=24-14=10 см.
Стороны треугольника 6 см, 8 см и 10 см.
Во втором случае, если один катет 40 см, второй будет 40+2=42 см и тогда периметр меньше, чем каждая из этих сторон и такого треугольника не существует.
Значит, задача имеет одно решение и стороны треугольника 6 см, 8 см и 10 см.