14
Пошаговое объяснение:
все числа кратны 7
ответ: 8π
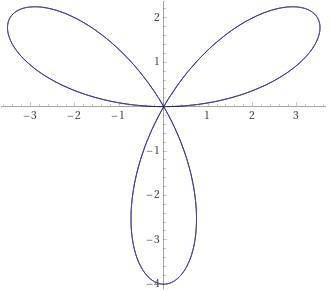
Пошаговое объяснение: r=4sin (3ф) это уравнение 3-х лепестковой розы в полярной системе координат.
Максимальное значение r=4, min r=0.
Период функции Sin (3ф)= 2π/3 Разделим на3 равные части лучами [0; 2π] в полярной системе координат, выполним рисунок (прилагается). Найдём площадь S₁ половины лепестка розы, а затем умножим на 6. Пределы интегрирования от 0 до π/6 ( у знака интеграла плохо видно)
S₁= 1/2·∫₀ⁿ⁾⁶(4sin(3ф))²dф= 1/2·∫₀ⁿ⁾⁶ 16sin²(3ф)dф=8·∫₀ⁿ⁾⁶sin²(3ф)dф=
4·∫₀ⁿ⁾⁶(1-сos(6ф)dф= 4·∫₀ⁿ⁾⁶dф - 4/6 ·∫₀ⁿ⁾⁶сos(6ф)d(6ф)=
=(4ф-sin(6ф))|₀ⁿ⁽⁶=2π/3 - sin(π)-0+0=2π/3
Значит S=6·S₁=6·(2π/3)=8π
35 - 28 = 7
28 - 21 = 7
Следовательно разница между числам - 7.
21 - 7 = 14
Пропущенное число - 14.