Р=(25+5)*2 P=(41+20)*2 Р=60 P=122 S=25*5 S=41*20 S=125 S=820
Исследование функции Y = X^3 + 6^2X + 9X.
1) Область определения:
Х€ (- ∞,+ ∞)
2) Пересечение с осью Х
Х= 0, Х = - 3.
3) Пересечение с осью У
У (0) = 0.
4) Поведение на бесконечности
У (- ∞) = - ∞
У (+ ∞) = + ∞
5) Исследование на четность
Y (+ x) = x^3 + 6x^2 + 9
Y (- х) = - х^3 + 6х - 9
Функция ни четная ни нечетная
6) Монотонность
Производная функции
Y' = 3x^2 + 12x + 9
Точки экстремумов
х1 = - 3 х2 = - 1.
Ymax (- 3) = 0
Ymin (1) = 4.
Возрастает Х€ (- ∞,- 3]∪[- 1,+ ∞)
Убывает X€ [- 3, - 1]
7) Точки перегиба - нули второй производной
Y" = 6x + 12 = 0
Х= - 2.
Выпуклая - "горка" - Х€(-∞;-2]
Вогнутая - "ложка" - Х€[-2;+∞)
Пошаговое объяснение:
Как то так.
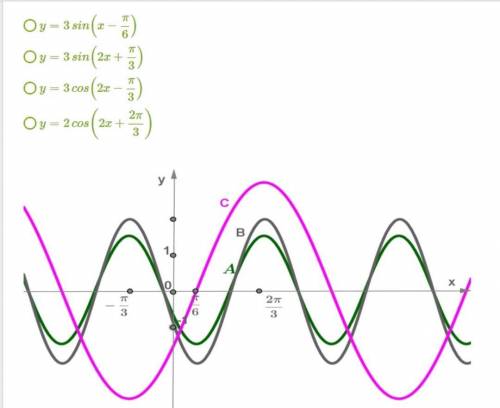
Первой функции. Потому что этот график проходит через точку пи/6.
Пошаговое объяснение: