Рисунок во вложении.
1. Нарисовать две прямые а и b.
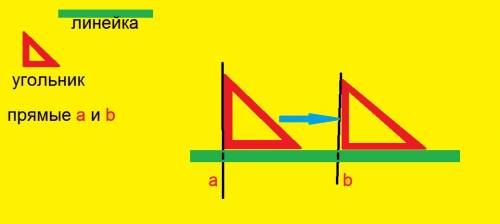
2. Совместить сторону (катет) прямого угла угольника с прямой а, а к другой стороне (катету) приложить линейку.
3. Двигать угольник по линейке до прямой b.
4. Проверить, если та сторона, которая была совмещена с прямой а, совмещается, также, и с прямой b.
Если совмещается, то прямые параллельны, если нет - то не параллельны.
На рисунке видно, что сторона угольника не совместилась с прямой b, значит эти прямые не параллельны.
ответ: построение параллельных прямых неточное, a ∦ b.
При данной проверке подтвеждается правило параллельности прямых: " Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны."
В роли третьей прямой выступает линейка, а угольник проверяет, если углы пересечения прямых а и b с линейкой равны.
849.
Пошаговое объяснение:
Справка:
Порядок действий в выражениях с несколькими действиями:
1. Выполняем действия I ступени (умножение и деление) в скобках.
2. Выполняем действия II ступени (сложение и вычитание) в скобках.
3. Выполняем действия I ступени (умножение и деление) за скобками.
4. Выполняем действия II ступени (сложение и вычитание) за скобками.
875 - 24 * 8 : 6 + ( 164 - 116 ) : 8
1) 164 - 116 = 48
2) 24 * 8 = 192
3) 192 : 6 = 32
4) 48 : 8 = 6
5) 875 - 32 = 843
6) 843 + 6 = 849
УДАЧИ! ОБРАЩАЙТЕСЬ!
а) у=2х; у'=2 в любой точке
б) у=х³+2; у'=3x
y'(5)=3*5=15; y'(8)=3*8=25
в) у=(x-2)²
y'=2*(x-2) * (x-2)'=2x-4
y'(5)=2*5-4=6
y'(8)=2*8-4=12
г) у=x^4+5x
y'=4x³+5
y'(5)=4*5³+5=4*125 + 5=505
y'(8)=4*8³ + 5=2053.