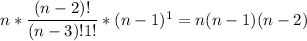Если одна прямая расположена в плоскости а, а другая прямая пересекает эту плоскость, то Через эти прямые прямые нельзя провести две различные плоскости.
p.s. остальные возможности перепробовала. Вот вам ещё пример из учебника.
Две прямые могут быть расположены в пространстве так, что через них нельзя провести плоскость.
Возьмём, например, две такие прямые АВ и DЕ, из которых одна пересекает некоторую плоскость Р, а другая лежит на ней, но не проходит через точку (С) пересечения первой прямой и плоскости Р.Через такие две прямые нельзя провести плоскость, потому что в противном случае через прямую и точку С проходили бы две различные плоскости: одна Р, пересекающая прямую АВ, и другая, содержащая её, а это невозможно.
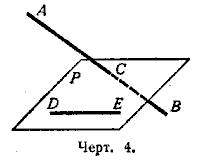
Т..к. dz/dx и dz/dy всегда существуют, то для нахождения стационарных (критических) точек получим систему уравнений:
dz/dx = 2x - 3y + 5 = 0
dz/dy = -3x - 2 = 0
Решаем систему уравнений: 2x - 3y + 5 = 0
-3x - 2 = 0
Откуда: x = -2/3 y = 11/9.
Таким образом получили стационарную точку M (-2/3; 11/9).
Находим: А = d2z/dx2 = 2, B = d2z/dxdy = -3, C = d2z/dy2 = 0 (запись d2z/dx2 означает "вторая производная функции z по x")
Тогда: D = AC - B*2 = -9. Итак в точке M (-2/3; 11/9) D = -9 < 0 - в этой точке экстремума нет.
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно