Пошаговое объяснение:
S=6a²
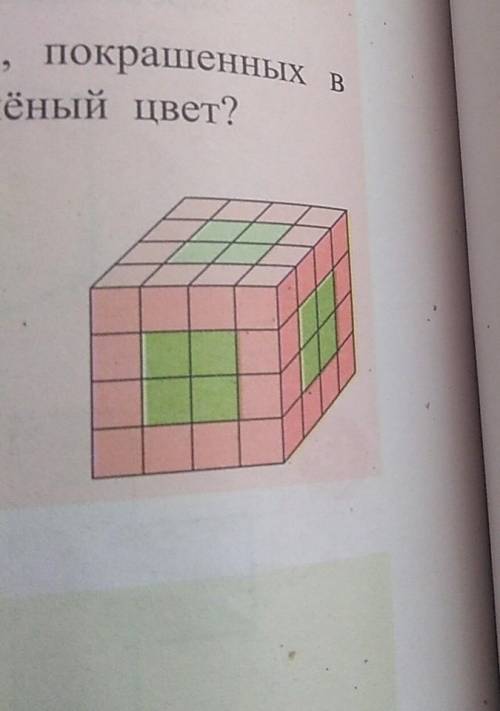
Sпол.пов.=12²*6=864 см² это поверхность всего куба и красного и зелёного вместе.
Грань 12см, а одна клетка грани это 12/4=3 см
Грань зелёного равна 2*3=6 см
Sзел.=6²*6=36*6=216 см²
Площадь красного куба равна разности между площадью полной поверхности куба и площади зелёного куба.
Sкр.=864-216=648 см²
Уже в ходе мирных переговоров обнаружились острые противоречия между римлянами и их союзниками.
Рим склонен был диктовать свои условия не только побеждённому Филиппу , но и своим союзникам, без поддержки которых он едва ли смог бы разбить македонян.
Судьба всех отнятых у Филиппа городов решалась римским сенатом и непосредственно сенатской комиссией, направленной в Грецию под председательством Тита Фламинина.
Требования союзников учитывались лишь в той мере, в какой это было выгодно римлянам.
На истмийских играх в 196 г. римляне с помпой провозгласили «свободу» всех эллинов.
В действительности же римляне по собственному усмотрению устанавливали границы греческих государств, передавая одни города Ахейскому союзу, другие — Этолийскому, третьи — царькам иллирийцев и их соседей афаманов.
Лицемерно объявив свободу Коринфа, римляне поставили свой гарнизон в его крепости Акрокоринфе.
Они оставили также под своей властью важные в стратегическом отношении города Деметриаду в Фессалии и Хал к иду на острове Эвбея.
Не создавая официально особой администрации для управления Грецией, Рим с сенатской комиссии и послов вмешивался в её внутреннюю жизнь.
Так, в Фессалии, где борьба между аристократией и демосом была настолько ожесточённой, что народные и судебные собрания постоянно сопровождались вооружёнными столкновениями, Фламинин провёл выборы совета и судей на основе цензового принципа и таким путём укрепил положение аристократии, иными словами, перестроил Фессалийскую лигу по образцу аристократического Ахейского союза.
Пока шла война с Филиппом, римляне заключили союз с правителем Спарты Набисом, но как только их положение в Греции несколько окрепло, они потребовали от других своих союзников объявления войны Набису, опять-таки под предлогом «освобождения» греческих городов от его «тирании».
В результате военных действий в 195 г. Набис вынужден был отказаться от Аргоса и других подвластных ему городов на побережье Пелопоннеса и от всех своих владений на Крите, ограничившись областью собственно Спарты.
В результате второй Македонской войны римляне захватили в Греции огромные богатства.
Только во время триумфа Фламинина демонстрировалось 18 270 фунтов серебра и 3 714 фунтов золота в слитках, 84 тыс. серебряных тетрадрахм и 14514 золотых «филиппиков», огромное количество медных и мраморных статуй, серебряных и золотых вещей, вывезенных из Греции.
Несомненно, что ещё большее количество ценностей было награблено римской армией.
Кроме того, греческие государства в благодарность за «свободу» вынуждены были отправить в Рим 114 золотых венков и вернуть купленных ими у карфагенян пленных римлян. Ахейскому союзу эти дары обошлись в 100 талантов.
Как позволяет заключить надпись из города Хиретии, римляне захватывали у побеждённых не только движимое имущество, но иногда и земельные владения и дома, возвращая их потом лишь за выкуп.
Естественно, что такая «освободительная» деятельность Рима вызвала недовольство широких слоёв греческого населения.
Против Рима открыто выступали этолийцы, обделённые римлянами при разделе владений Филиппа. Весьма неуверенно чувствовали себя проримские группировки в Беотии.
Недовольство это особенно ярко проявилось, когда на Балканском полуострове высадился со своим войском Антиох III.
Площадь, закрашенная красным по всей поверхности куба, равна 648 см².
Площадь, закрашенная зеленым по всей поверхности куба, равна 216 см².
Пошаговое объяснение:
Так как одно ребро равно 12 см, то длина стороны маленького кубика равна 12:4=3 см. Так как всего 4 кубика по длине грани. Теперь по одной стороне квадрата красных квадратов всего 4+4+2+2=12. А зеленых: 4.
По одной стороне куба площадь, закрашенная красным, равна: 3*3*12=108 см². А всего граней у куба 6. Значит площадь, закрашенная красным, равна 108*6=648 см².
По одной стороне куба площадь, закрашенная зеленым, равна 3*3*4=36 см². А всего граней у куба 6. Значит площадь, закрашенная зеленым, равна: 36*6=216 см².