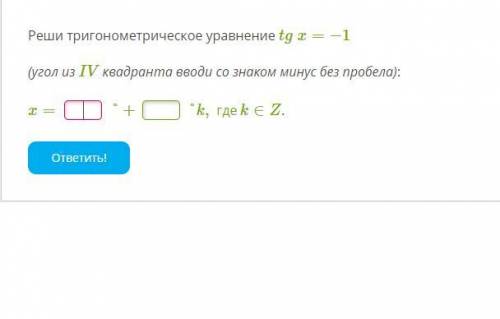
6 см
Пошаговое объяснение:
По условию, трапеция вписана в окружность, значит она равнобедренная, т.е. CD=AB (это свойство трапеции).
Центр О окружности лежит на AD - большем основании трапеции, значит, сторона AD - диаметр трапеции ABCD, а отрезок AO является радиусом трапеции.
Найдём радиус окружности:
r = D/2 = AD/2 =12/2 = 6 см
AO= r = 6 см
Отрезок ОВ = 6 см, т.к. он также является радиусом окружности.
ΔАОВ - равнобедренный, т.к. АО=ОВ=r=6 см.
В равнобедренном треугольнике углы при основании равны, поэтому ∠ОАВ=∠ОВА.
По условию, ∠А=60°. ∠А=∠ОАВ, следовательно, ∠ОВА=60°.
Найдём ∠АОВ:
∠АОВ=180°-(∠ОАВ+∠ОВА)=180°-(60°+60°)=180°-120°=60°
Получается, что ΔАОВ - равносторонний.
Это означает, что АВ=ОА=ОВ=6 см
Т.к. трапеция равнобедренная, то CD=AB=6см
578384837573748287471836373737199583747484837583838582759482749927481947377737288847474*74747384727601957584737763383948277495038482758488374837473737473737738292037472728374799294839218183949284994828399383838283939939384848485738329201054843838293049292030209919383718483881848838728
578384837573748287471836373737199583747484837583838582759482749927481947377737288847474*74747384727601957584737763383948277495038482758488374837473737473737738292037472728374799294839218183949284994828399383838283939939384848485738329201054843838293049292030209919383718483881848838728
578384837573748287471836373737199583747484837583838582759482749927481947377737288847474*74747384727601957584737763383948277495038482758488374837473737473737738292037472728374799294839218183949284994828399383838283939939384848485738329201054843838293049292030209919383718483881848838728