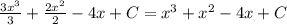НОК (Наименьшее общее кратное) 320 и 450
Наименьшим общим кратным (НОК) 320 и 450 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (320 и 450).
НОК (320, 450) = 14400
Как найти наименьшее общее кратное для 320 и 450
Разложим на простые множители 320
320 = 2 • 2 • 2 • 2 • 2 • 2 • 5
Разложим на простые множители 450
450 = 2 • 3 • 3 • 5 • 5
Выберем в разложении меньшего числа (320) множители, которые не вошли в разложение
2 , 2 , 2 , 2 , 2
Добавим эти множители в разложение бóльшего числа
2 , 3 , 3 , 5 , 5 , 2 , 2 , 2 , 2 , 2
Полученное произведение запишем в ответ.
НОК (320, 450) = 2 • 3 • 3 • 5 • 5 • 2 • 2 • 2 • 2 • 2 = 14400
Пошаговое объяснение:
Движение в противоположных направлении.
Выехал велосипедист и вышел пешеход из одного поселка одновременно.
Скорость велосипедиста 16 км/ч.
Скорость пешехода 4 км/ч.
Время движения 3 ч.
Определить расстояние между ними.
Определим расстояние, которое проехал велосипедист и пешеход по формуле:
S = v * t, где
S — пройденный путь (км),
v — скорость движения (км/ч),
t — время (ч), за которое пройден путь S.
Расстояние, которое проехал велосипедист за 3 часа:
S1 = 16 * 3 = 48 км.
Расстояние, которое пешеход за 3 часа:
S2 = 4 * 3 = 12 км.
Согласно условию задачи, что велосипедист и пешеход вышли одновременно с одного поселка и разных направлениях, то можем определить расстояние между ним после 3 часов движения:
S3 = S1 + S2, км
S3 = 48 + 12 = 60 км.
ответ: расстояние между велосипедистом и пешеходом после 3 часов движения будет 60 км.
Відповідь:
Покрокове пояснення:
F(x)=