Question

Объясните почему (ответ впишите сюда) Можно ли число 17 представить в виде суммы двух чисел так, чтобы их произведение было равно сор

Answer 1

нет.

Пошаговое объяснение:

1*16=16

2*15=30

3*14=42

4*13=52

5*12=60

6*11=66

7*10=70

8*9=72

Answer 2

Решений нет

Пошаговое объяснение:

Следуя из условия, можно создать систему уравнений: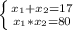
$\left \{ {{x_{1}+x_{2} =17} \atop {x_{1}*x_{2} =80}} \right.$
Решим эту систему:
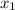
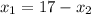
Выразим, например,$x_{1}$
$x_{1} =17-x_{2}$
Подставим переменную в второе уравнение, получим: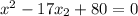

$x^{2} -17x_{2}+80=0$

При решении этого квадратного уравнения видим, что дискриминант меньше нуля: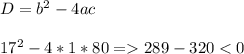

$D=b^2-4ac\\ \\ 17^2-4*1*80= 289-320$

Это значит, что график функции не пересекает ось x,следовательно решений квадратного уравнение нет, а значит, и системы