Сначала выберем каких-нибудь троих красных хамелеонов. Так как они все не сидят на одной прямой, они сидят в вершинах треугольника. Пусть данный треугольник не удовлетворяет условию задачи, тогда на его сторонах есть хотя бы три синих хамелеона. Так как эти три синих хамелеона не сидят на одной прямой, они сидят в вершинах треугольника, площадь которого меньше площади предыдущего. Если новый треугольник снова не удовлетворяет условию задачи, выберем аналогичным образом (на сторонах нового треугольника) ещё один. Так как каждый последующий треугольник по площади меньше предыдущего, когда-нибудь этот процесс остановится. Полученный в конце треугольник удовлетворяет условию задачи.
Существует. Более того, формулируя строгим языком: для любого натурального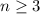 существует последовательность из
существует последовательность из  подряд идущих составных чисел.
подряд идущих составных чисел.
Действительно, каждое из чисел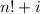 , где
, где 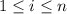 делится на
делится на  , и при этом
, и при этом 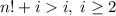 .
.
Взяв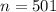 , получим 500 составных чисел:
, получим 500 составных чисел: 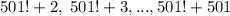 .
.