Один или два.
Пошаговое объяснение:
Предположим, какой-то рыцарь сказал вторую фразу. Тогда оба его соседа – рыцари. Рассмотрим его соседа справа. Он рыцарь, и слева от него сидит рыцарь. Он не может солгать, сказав первую фразу, и должен сказать, что оба его соседа – рыцари. Тогда рассмотрим его соседа справа; и так далее. Получается, что все присутствующие за столом – рыцари, чего быть не может. Значит, все присутствующие рыцари обязаны говорить первую фразу, а таких фраз всего две. Следовательно, рыцарей не более двух.
Правильная четырёхугольная пирамида.
FG = 6 (см).
FH = 10 (см).
Найти:AB = ? (см).
Решение:В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому все стороны в основании будут равны.
Когда мы опустили высоту к основанию и провели апофему к боковой грани нашей пирамиды, то у нас образовался прямоугольный △FGH, где FH - гипотенуза прямоугольного треугольника (апофема пирамиды), GH - катет прямоугольного треугольника, FG - катет прямоугольного треугольника (высота пирамиды).
Мы сможем найти длину катета GH по теореме Пифагора (a = √(c² - b²), где a и b - катеты, c - гипотенуза).
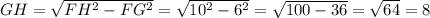 (см).
(см).
Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырёхугольной пирамиды.
Т.е. GH = HC = DH = 8 (см).
Так как апофема по свойству делит сторону основания пирамиды пополам, то:
 (см).
(см).
 (см).
(см). 
E) 47
Пошаговое объяснение:
Чисел кратных 3 в указанном интервале 33 шт.
Чисел кратных 5 - 20 шт.
Среди них есть числа, которые делятся и на 3 и на 5, т.е на 15. Эти числа мы учли дважды. Таких чисел 6.
ответ: 33+20-6=47