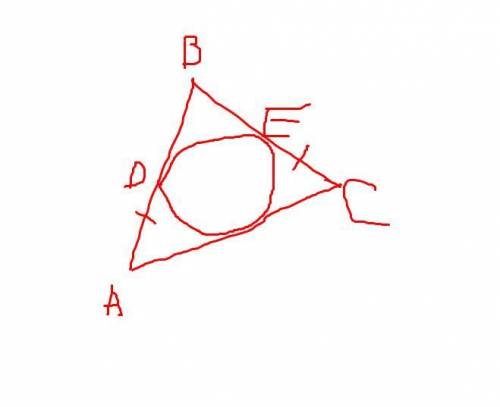
Чертеж с тем, что нам дано изначально, в прикрепленных файлах.
По условию дано, что AD=EC. Интересующие нас стороны - это AB и BC. Равные по условию отрезки являются их частями => AB-BD=BC-BE.
Поэтому для доказательства равенства AB и BC нам нужно лишь доказать равенство отрезков BD и BE.
AB и BC треугольника ABC являются двумя касательными к окружности, причем из 1 точки B. Применяем свойство двух касательных к окружности из 1 точки: Если две касательные к одной окружности исходят из 1 точки, то равны отрезки из этой точки до самой окружности. BD и BE - это отрезки из B до окружности => они равны.
1) 857 x 308=263956
2) 300000-263956=36044
3) 166704 : 276=604
4) 4 731 075 : 675=7009
5) 36044:4=9011
6) 9011х800=7208800
7) 604х7009=4233436
8) 7208800-4233436=2975364
2. 2 500 000 : 500 x (3784 + 0 x 5863) - (703 -703) : 29 + 80 x 2000=19080000
1) 0 x 5863=0
2) 3784 + 0=3784
3) 703 -703=0
4) 2 500 000 : 500=5000
5) 5000*3784=18920000
6) 0:29=0
7) 80 x 2000=160000
8) 18920000-0=18920000
9) 18920000+160000=19080000