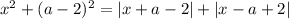
Рассмотрим правую часть уравнения.
Найдем нули модулей:
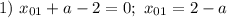
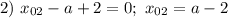
Тогда 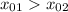 при
при 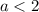 и
и 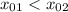 при
при 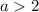 .
.
➠ Если 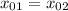 , то есть если
, то есть если 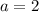 , то имеем:
, то имеем:
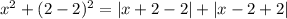
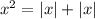
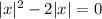
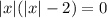
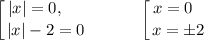
Имеем три корня. Таким образом, вариант 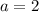 не подходит.
не подходит.
➠ Если 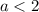 , то:
, то:
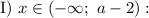
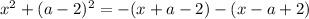
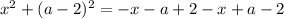
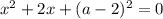
Имеем квадратное уравнение. Для того чтобы это уравнение имело один корень, нужно чтобы дискриминант данного уравнения был равен нулю:
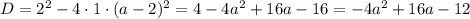
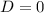 при
при 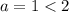 и
и 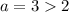
Таким образом, при 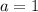 имеем решение.
имеем решение.
![\text{II}) \ x \in [a - 2; \ 2 - a]:](/tpl/images/1357/3941/2f10d.png)
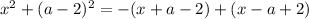
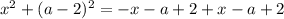
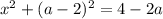
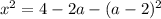
Данное квадратное уравнение будет иметь один корень, если его правая часть будет равна нулю:
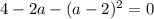
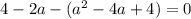
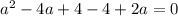
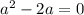
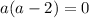
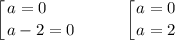
Таким образом, при 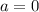 имеем единственное решение.
имеем единственное решение.
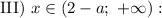
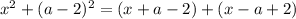
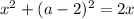
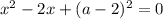
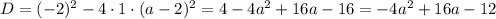
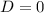 при
при 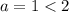 и
и 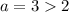
Таким образом, при 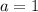 имеем решение.
имеем решение.
Следовательно, при 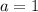 имеем два решения.
имеем два решения.
➠ Если 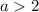 , то:
, то:
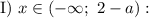
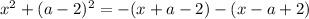
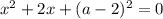
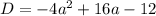
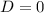 при
при 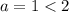 и
и 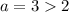
Таким образом, при 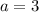 имеем решение.
имеем решение.
![\text{II}) \ x \in [2 - a; \ a - 2]:](/tpl/images/1357/3941/aa9bc.png)
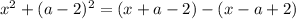
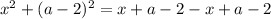
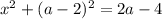
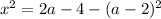
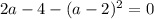
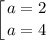
Таким образом, при 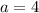 имеем единственное решение.
имеем единственное решение.
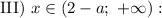
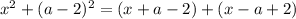
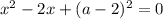
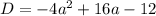
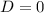 при
при 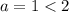 и
и 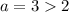
Таким образом, при 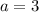 имеем решение.
имеем решение.
Следовательно, при 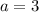 имеем два решения.
имеем два решения.
ответ: 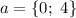

Вопрос 1.
1. Семенами размножается:
2. мох
3. плаун
4. папоротник
5. сосна
Вопрос 2.
Растения растущие сами по себе в природе:
1. культурные
2. дикорастущие
3. светолюбивые
Вопрос 3.
Процесс фотосинтеза характерен для представителей царства:
1. животные
2. растения
3. грибы
4. вирусы
Вопрос 4.
Группа растений, тела которых не имеют ни тканей, ни органов, называется:
1. водоросли
2. папоротники
3. голосеменные
4. цветковые
Вопрос 5.
Семена ели созревают:
1. в почках
2. на листьях
3. в шишках
4. в плодах
Вопрос 6.
Зелёный пигмент растения:
1. ксантофил
2. хлорофилл
3. хромопласт
Вопрос 7.
Тело водоросли называется:
1. орган
2. хламидомонада
3. органоид
4. слоевище
Вопрос 8.
Преобладают древесные и кустарниковые формы среди растений:
1. папоротников
2. голосеменных
3. хвощей
4. мхов
Вопрос 9.
Древнейшая профессия человека, который занимался выращиванием растений для себя:
1. лесовод
2. полевод
3. земледелец
Вопрос 10.
Для мхов характерно наличие:
1. цветков и плодов
2. корней
3. проводящих тканей
4. стеблей и листьев
Вопрос 11.
Верны ли следующие утверждения?
А. Органами размножения хвойных деревьев являются цветки и плоды.
Б. Клетки листьев ели вырабатывают кислород в ходе фотосинтеза.
1. верно только А
2. верно только Б
3. верны оба суждения
4. неверны оба суждения