![Найдите наибольшее и наименьшее значения функции y = f (x) на отрезке [a, b]](/tpl/images/3775/8799/eee50.jpg)
Y(X)наиб = -1
Y(X)ним = 4
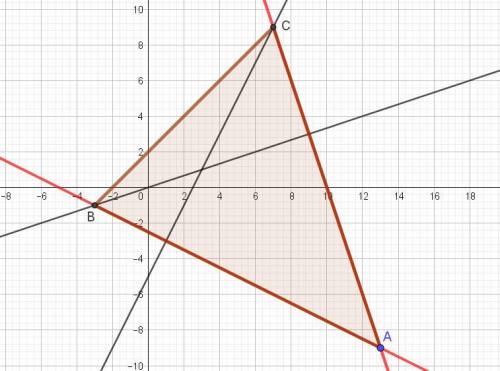
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
-1
Пошаговое объяснение:
Чтобы найти наиболшее и наименшее значение на заданном отрезки первоначально поставим на функции самые крайные значение отрезки то ест: - 1 и 4
y(-1)= - (-1)-4/(-1+2)^2= 1-4=-3
y(4)= - (4)-4/(4+2)^2=-4-1/9=-37/9
Второе найдем экстремумы функции:
y'=(-x-4/(x+2)^2)'=-1+(2x+4)(x+2)^2/(x+2)^4=-1+2/(x+2)=0 x=0 поставим это на заданную функцию: y(0)=-1
Самая болшая значение это -1