Составим вектора имеющие начало в точке A, а конец в B или C:
AB = {2, -3, 6}
AC = {6, 2, -3}
Скалярное произведение:
AB * AC = 12 - 6 - 18 = -12
AB*AC ≠ 0, значит вектора не перпендикулярны
Найдем длины векторов:
|AB| =
|AC| =
Пусть - искомый угол (он же угол между векторами АВ и АС)
Приравняем скалярное произведение через длины к скалярному произведению через координаты:
|AB| * |AC| * cos = -12
Выразим косинус угла
cos = =
Выразим через обратную тригонометрическую функцию
=
Примечание:
Найти этот арккосинус можно с калькулятора, окажется что наш искомый угол равен примерно 104°. Также это проверяется построением треугольника в системе координат.
1) Числа, которые при делении на 5 дают в остатке 4 должны заканчиваться либо на 9, либо на 4. Это числа: 9, 14, 19, 24, 29, 34 и т.п. 2) число делится на 3 без остатка, если сумма цифр, составляющих это число делится на 3. Значит, чтобы при делении на три получался остаток 2, надо, чтобы число, сумма цифр, составляющих искомое число за вычетом 2 делилось на 3. Исключаем числа, которые делятся без остатка на 3 (смотри числа в пункте 1)). Остаются: 14, 19, 29, 34 и т.п. Вычитаем поочередно из чисел 2 и смотрим, делится ли разность на 3 без остатка: 14-2=12 делится без остатка на 3 19-2=17 не делится на 3 29-2=27 делится без остатка на 3 34-2=32 не делится на 3 И т.д Но уже видно, что искомое число 14 Оно минимальное из натуральных чисел, удовлетворяющее условию задачи. ответ: 14
Пошаговое объяснение:
Составим вектора имеющие начало в точке A, а конец в B или C:
AB = {2, -3, 6}
AC = {6, 2, -3}
Скалярное произведение:
AB * AC = 12 - 6 - 18 = -12
AB*AC ≠ 0, значит вектора не перпендикулярны
Найдем длины векторов:
|AB| =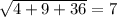
|AC| =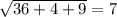
Пусть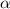
- искомый угол (он же угол между векторами АВ и АС)
Приравняем скалярное произведение через длины к скалярному произведению через координаты:
|AB| * |AC| * cos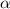
= -12
Выразим косинус угла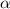
cos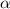
= 
= 
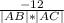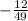
Выразим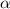
через обратную тригонометрическую функцию
Примечание:
Найти этот арккосинус можно с калькулятора, окажется что наш искомый угол равен примерно 104°. Также это проверяется построением треугольника в системе координат.