ответ:1) Чтобы не запутаться, обозначим возраст сестры сейчас через С, а возраст брата через Б. Так им обоим сейчас 26 лет, то можем составить уравнение, а именно: С + Б = 26 ― 1 -ое уравнение.
2) Через какое-то количество лет, обозначим это количество через Х, возраст брата будет (Б + Х), а возраст сестры будет (С + Х), их общий возраст будет в 5 раз больше, чем возраст брата сейчас, поэтому можем записать: (Б +Х) + (С + Х) = 5Б или С - 4Б + 2Х = 0 ― 2-ое уравнение.
3) Через Х лет возраст брата будет в 3 раза больше, чем возраст сестры сейчас, поэтому можем записать: 3С = Б + Х ― 3-е уравнение
4) Таким образом получается система из 3 уравнений с тремя неизвестными. Решаем систему. Из первого уравнения выражаем Б, получаем Б = 26 - С и подставляем в третье уравнение, получаем:
3С = 26 - С + Х Отсюда находим Х = 4С - 26 , затем значение Х подставляем во второе уравнение, получаем:
С - 4(26 - С) + 2(4С -26) = 0
С - 104 + 4С + 8С - 52 = 0
13С = 156 Отсюда С = 12 - это возраст сестры
Б = 26 - 12 = 14 - это возраст брата.
ответ: сестре - 12 лет, брату - 14 лет
Пошаговое объяснение:
Если доска 3х3, то выстрел в центральную клетку этого квадрата гарантированно попадет в корабль 2х2, вне зависимости от его расположения на доске.
Таким образом, одну клетку мы гарантированно определили без выстрела. (Конечно, в том случае, если на этом поле точно есть корабль..)))
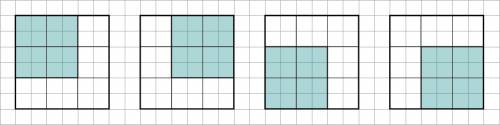
Варианты расположения корабля на доске - см. рис.
Первым выстрелом, допустим, в нижнюю среднюю.
Если попали, - вторым выстрелом бьем в левую или правую
нижние.
Если не попали, - в левую или правую верхние.
По результату определяем точное положение.
Итого: 2 выстрела.
Здесь действует так называемая лемма о рукопожатиях.
Рассмотрим граф, вершины которого являются учениками. Между двумя учениками проведем ребро, если они знакомы.
Просуммируем степени вершин. Поскольку каждое ребро имеет ровно две вершины, сумма степеней вершин будет равна удвоенному количеству ребер, однако для нас важнее то, что эта сумма четна.
Поскольку сумма вершин, имеющих четную степень четна, то и сумма вершин, имеющих нечетную степень также четна. Поэтому количество вершин с нечетной степенью четно.
Назовем учеников, имеющих четное кол-во знакомых четными, а нечетное — нечетными.
Заметим, что Гоша не получит подзатыльник только от знакомых, имеющих нечетное количество знакомых. Пусть их
. Пусть всего 
учеников, тогда Гоша получит 
подзатыльников. Уберем Гошу из рассмотрения. Тогда нечетные знакомые станут четными, нечетные незнакомые останутся нечетными, а четные знакомые станут нечетными. Поэтому сумма количества четных знакомых с нечетными незнакомыми, равная 
, равна четному числу (после применения леммы). Итак, Гоша получит четное количество подзатыльников. Поскольку он получил 99, его ожидает еще какое-то нечетное количество