Пошаговое объяснение:
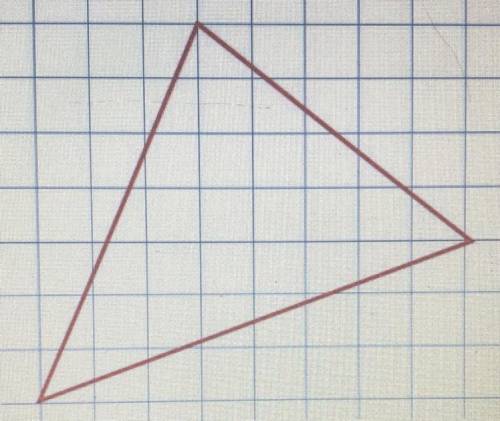
1) Если по клеточкам поместить треугольник в квадрат так, чтобы вершины треугольника лежали на трех сторонах квадрата, то получим квадрат со стороной 5 клеточек.
2) Лего увидеть, то площадь искомого треугольника можно вычислить, если из площади квадрата вычесть площади трех прямоугольных треугольников, образованных сторонами квадрата и сторонами искомого треугольника.
Площадь прямоугольного треугольника:
S = ab/2, где a и b - катеты.
3) Sквадрата = 5•5 = 25 клеточек.
4) Sлевого треугольника = (5•3)/2 =
= 15/2 = 7,5 клеточек.
5) S верхнего правого треугольника =
= (2•4)/2 = 4 клеточки.
6) Sнижнего треугольника = (1•5)/2 = 2/5 клеточки.
7) Sискомого треугольника =
= 25 - (7,5 + 4 + 2,5) = 25 - 14 = 11 клеточек
Пошаговое объяснение:
Пусть ширина комнат - а cм, тогда по условию длина первой комнаты в 1,5 раза больше ширины и равна 1,5а, длина второй комнаты равна 7,5 м . Площадь равна 36м², отсюда имеем S=a*b
36 = 1,5a*а + ab
36 = 1,5a² + 7,5a
1,5a² + 7,5a - 36=0
D = b²- 4ac = 7,5²- 4 *1,5*(-36)=√56,25+216=√272,25 =16,5
a₁=(-b -√D)/2a=(-7,5-16,5)/2*1,5= -24/3= -8 м < 0 - не удовлетворяет условию.
a₂= (-b+√D)/2a =(-7,5+16,5)/2*1,5= 9/3= 3 м
И так ширина этих комнат 3 м
Проверка : Площадь одной комнаты 3*7,5= 22,5 м²
длина первой комнаты 3*1,5=4,5 м
Площадь второй 3*4,5=13,5м²
Площадь комнат 22,5+13,5= 36м²
площадь S=376м²
1 клетка 4м
стороны треугольника находим через теорему Пифагора .
треугольник вписан в прямоугольник из клеток с размером в длину 8 и ширину 7 клеток.
треугольник ΔACE вписанный в четырёхугольный прямоугольник □ ABDF , образует прямоугольные треугольники ΔABC где<В=90° , ΔCDE где <D=90° и
ΔAFE где <F=90°.
AF=BC+CD ,
AB=DE+EF ,
BC=3 кл ,
CD=5 кл ,
AF=8 кл ,
DE=4 кл ,
EF=3 кл ,
AB=7 кл.
переводим на метры
BC=3×4=12м,
CD=5×4=20м,
AF=8×4=32м,
DE=4×4=16м,
EF=3×4=12м ,
AB=7×4=28м .
по теореме Пифагора находим для каждого прямоугольного треугольника гипотенузы, которые являются в свою очередь сторонами ΔACE.
для ΔABC
AC=√AB²+BC²=√28²+12²=√784+144=√928
для ΔCDE
CE=√CD²+DE²=√20²+16²=√400+256=√656
для ΔAFE
AE=√AF²+EF²=√32²+12²=√1024+144=√1168
находим площадь прямоугольных треугольников
ΔABC
S1=ab/2= AB×BC/2=28×12/2=168 м²
ΔCDE
S2=CD×DE/2=20×16/2=160 м²
ΔAFE
S3= AF×EF/2=32×12/2=192 м²
площадь четырёхугольника □ABDF
S□=a×b=AB×AF=28×32=896 м²
площадь четырехугольника равна сумме площадей треугольников ΔACE, ΔABC , ΔCDE и ΔAFE:
S□=SΔACE +S1+S2+S3 ,
отсюда можно найти площадь ΔACE
SΔACE= S□- (S1+S2+S3),
SΔACE=896 - (168 + 160 + 192)=896 - 520 = 376м²
периметр участка, треугольника ΔACE
P=AC+CE+AE=√928 +√656 +√1168 = округленно 90,25 м