![CРОЧНО Решите систему уравнений [фото ниже] (Желательно, либо прислать фото решения, либо прислать](/tpl/images/3776/8465/a4969.jpg)
В современном мире чеканится большое количество всевозможных юбилейных и памятных монет. Они «оседают» в основном в коллекциях нумизматов и инвесторов, справедливо считающих, что сегодняшняя даже не очень редкая монета через несколько лет подорожает. А если в коллекциях монеты из драгоценных металлов украшены ещё и драгоценным камнем, то прибыльность вложений гарантирована. Особенно, если это натуральный алмаз или бриллиант. И вот такими монетами обзавелись двенадцать стран.Источник: https://mining-media.ru/ru/article/history-of-niming/kulturnoe-nasledie/13021-almazy-i-brillianty-na-monetakh-stran-mira
ответ: 
Пошаговое объяснение:
![\sqrt{12+\sqrt{12+\sqrt[]{20+4x+x^2} } } =x^2+4x+8\\x^2+4x+8 = (x+2)^2+4 = t\geq4 \\\sqrt{12+\sqrt{12+\sqrt[]{12+t} } } = t](/tpl/images/1361/5392/9b8b4.png)
Пусть:
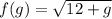
Тогда уравнение принимает вид:
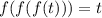
Заметим, что если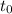 
корень уравнения 
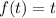, то он и корень уравнения:
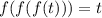, действительно:
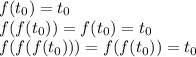
Найдем все такие корни:
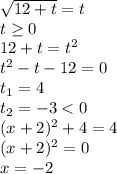
Заметим, что функция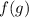 
- монотонно возрастает.
Предположим, что в уравнении 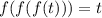существует корень 
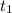, такой, что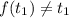 
Рассмотрим случай: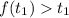 
.
Поскольку, 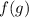- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 
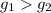, то верно и данное неравенство: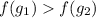 
Из данного утверждения следует, что :
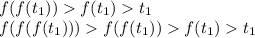
Но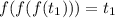 
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая
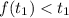. Таким образом, других корней помимо нет.
............................