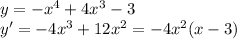
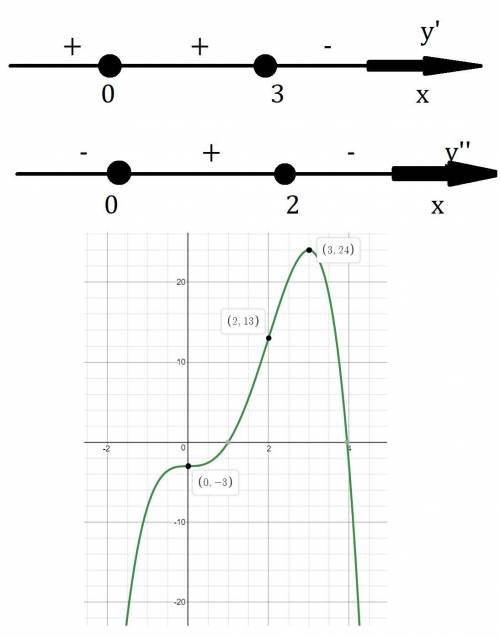
Как видно производная обращается в ноль при x=3 и x=0 это критические точки, используем метод интервалов, для определения знака производной на промежутках.
При x=0, производная не меняет знак, значит это не экстремум функции. При x=3, производная меняет знак с плюса на минус, значит это минимум функции.
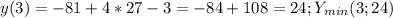
На (-∞;0)∪(0;3) функция растёт.
На (3;+∞) функция убывает.
Функция общего вида (не обладает чётность или нечётностью)
Найдём точки перегиба функции.
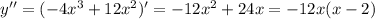
x=0 и x=2 это точки перегиба.
На (-∞;0)∪(2;+∞) функция выпукла вверх.
На (0;2) функция выпукла вниз.
Найдём координаты всего чего ещё не нашли.
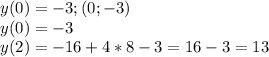
Можем строить.
Наименьшее значение (-∞;-∞) и (+∞;-∞)
Наибольшее значение (3;24)
дана эта формуланужно исследовать её на монотонностьнайти н" />
x-загаданное число (двухзначное)
a - целая часть после деления 462 на x
b - целая часть после деления 307 на x
462-x*a=остаток
307-x*b=тот же остаток, значит можно сказать, что
462-x*a=307-x*b; 155-x*a= -x*b; 155=x*a-x*b=x(a-b)
a и b это натуральные числа т.к. деление с остатком, значит и их разность будет натуральным числом и раз уж x - двухзначное, значит оно тоже натуральное (смысл в том, что числа без всяких десятичной дроби: 25,02)
Кстати да, получаем, что число 155 должно делиться нацело на x и (a-b)
Осталось разложить на простые числа и понять какие значения могут принимать наши неизвестные.
155=5*31 собственно это всё. Значит x=31 и (a-b)=5, нам надо было найти только x.
ответ: 31.