Пусть скорость работы 1 бригады - х а второй у Вся работа = 1 запишем уравнение {1/х=15 x=1/15 {1/(х+у)=12 x+y=1/12
1/15+y=1/12 y=1/12 - 1/15 у=(15-12)/(180) у=3/180=1/60 тогда время работы отдельно второй бригады 1/(1/60)=60 дней. 2) Пусть скорость первой девочки 1/15 тогда второй 1/10 Все расстояние = 1 Найдем время встечи t=1/(1/15+1/10)=1/(5/30)=6 минут 3) Пусть скорость первой трубы 1/2 тогда второй 1/4 время = 1 час. Найдем какую часть бака наполнят трубы (1/2 +1/4)*1=3/4 бака заполнят трубы за 1 час. Все задачи решаются по одной формуле движения S=V*t. V=S/t Всю работу или расстояние, или весь бак принимаем S=1/
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
Приведем к ступенчатому виду. Применяем операцию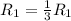 к
к  (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию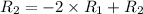 к
к  (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию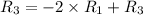 к
к  (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию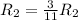 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию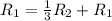 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Применяем операцию к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию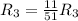 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию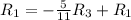 к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию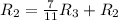 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
Решением является множество упорядоченных пар, которые удовлетворяют системе.