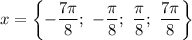Пусть x пирожков купил Коля, тогда 2x пирожков купил Вася, а Женя получается купил y пирожков при условии, что x<y<2x.
x+2x+y=14
3x+y=14
y=14-3x
Значение y подставляем в неравенство и получим: x<14-3x<2x
4x<14<5x
только при x=3, верно данное неравенство
Значих Коля купил 3 пирожка, 6 пирожков купил Коля и Женя купил 14-9= 5 пирожков
Пусть Коля купил х пирожков, тогда Вася 2х пирожков, а Женя у пирожков, причем х < y < 2x
Составим уравнение: х + 2х + у = 14;
3х + у = 14
3х = 14 - у.
Выражение 14 - у должно делиться на 3: числа до 14, делящиеся на 3 - это 12, 9, 6, 3.
Исследуем все варианты:
1) 14 - у = 12, тогда у = 2; 3х = 12; х = 4; 2х = 8; 4 < 2 < 8 (ложь)
2) 14 - у = 9, тогда у = 5; 3х = 9; х = 3; 2х = 6; 3 < 5 < 6 (истина)
3) 14 - у = 6, тогда у = 8; 3х = 6; х = 2; 2х = 4; 2 < 8 < 4 (ложь)
4) 14 - у = 3, тогда у =11; 3х = 3; х = 1; 2х = 2; 1 <11 < 2 (ложь)
Видим, что подходит только вариант 2), следовательно, Коля купил 3 пирожка, Вася 6 пирожков, а Женя 5 пирожков.
Предел последовательности. Раскрытие неопределенности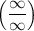 (с примером).
(с примером).
Число называется границей числовой последовательности
называется границей числовой последовательности 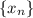 , если для любого
, если для любого 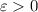 существует такой номер
существует такой номер 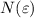 , что для всех
, что для всех 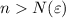 выполняется неравенство
выполняется неравенство 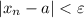
Символично это записывается так: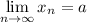 или
или  при
при 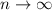
Для вычисления границ функций, заданных отношением двух многочленов в случае неопределенности типа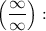
а) в числителе и знаменателе выносится в наивысшей степени. После соответствующих сокращений и, учитывая, что дроби типа
в наивысшей степени. После соответствующих сокращений и, учитывая, что дроби типа 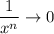 при
при 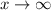 , получаем значение рассматриваемой границы;
, получаем значение рассматриваемой границы;
б) используются эквивалентные бесконечно большие, то есть
Тогда
При вычислении дробей, которые содержат иррациональность, выполняются аналогичные приемы.
Пример: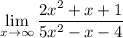
Решить уравнение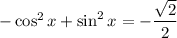 и отобрать его корни, принадлежащие промежутку
и отобрать его корни, принадлежащие промежутку ![[-\pi; \ \pi]](/tpl/images/1356/7292/6239f.png)
Отбираем корни, принадлежащие промежутку![[-\pi; \ \pi]:](/tpl/images/1356/7292/ed7a0.png)
Таким образом:
ответ: