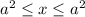 написать не только решение, но и максимально понятное объяснение !
написать не только решение, но и максимально понятное объяснение !Решение простое. х ≥ а², когда х либо больше, либо равно а².
Другая часть неравенства х ≤ а², когда х либо меньше, либо равно а².
Пересечение решений, т.е. их общее решение х=а² и будет ответом. а²≤а²≤а², т.е. при х=а² выполняется как одна часть неравенства, так и другая, поэтому х=а²
ответ х=а²
1)по теореме косинусов AB^2 = BC^2 AC^2 - 2*BC*AC*cosC = 5^2 32 - 40 = 17
2)ав^2=b^2+121+11*b значит ав=b+11 я подставила в формулу и упрастила выражение получился ответ в+11
2 a^2=b^2+c^2-2cosa вытащим отсюда соs, cos=(b^2+c^2-a^2)/2bc=(100+225-81)/2*10*15=61/75 -это я нашла косинус первого угла
b^2=a^2+c^2-2cosb cosb =(a^2+c^2-b^2)/2ac=(a^2+c^2-b^2)/2ac=9^2+15^2-10^2/2*9*15=81+225-100/270=206/270=103/135- это я нашла второй косинус угла
с^2=a^2+в^2-2cosс cosс =(a^2+в^2-с^2)/2aв=9^2+10^2-15^2/2*9*10=81+100-225/180 - это я нашла косинус третьего угла.
1)по теореме косинусов AB^2 = BC^2 AC^2 - 2*BC*AC*cosC = 5^2 32 - 40 = 17
2)ав^2=b^2+121+11*b значит ав=b+11 я подставила в формулу и упрастила выражение получился ответ в+11
2 a^2=b^2+c^2-2cosa вытащим отсюда соs, cos=(b^2+c^2-a^2)/2bc=(100+225-81)/2*10*15=61/75 -это я нашла косинус первого угла
b^2=a^2+c^2-2cosb cosb =(a^2+c^2-b^2)/2ac=(a^2+c^2-b^2)/2ac=9^2+15^2-10^2/2*9*15=81+225-100/270=206/270=103/135- это я нашла второй косинус угла
с^2=a^2+в^2-2cosс cosс =(a^2+в^2-с^2)/2aв=9^2+10^2-15^2/2*9*10=81+100-225/180 - это я нашла косинус третьего угла.
Чтобы было нагляднее, вычтем из всех частей этого неравенства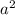 :
:
Выражение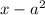 не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел
не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел  и
и 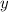 выполняется одно и только одно из соотношений:
выполняется одно и только одно из соотношений: 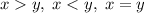 ), поэтому оно может равняться только нулю:
), поэтому оно может равняться только нулю:
В мат. анализе с приведения к подобному неравенству (только для функций) доказывается существование первого замечательного предела - "теорема о двух конвоирах (миллиционерах)"