Пример для пяти очевиден: все диагонали из одной вершины. Пример для семи: возьмем квадрат, проведя в нем все диагонали. После этого "облепим" его одинаковыми треугольниками (так, чтобы их внутренние углы были не 45 градусов) с трех сторон.
Пусть треугольников разбиения . Будем вырезать их, но на каждом ходу будем вырезать только такой, у которого хотя бы одна сторона является стороной многоугольника. Тогда количество сторон либо увеличивается на 1, либо уменьшается на 1, либо даже уменьшается на 3. Все эти числа нечетны. Поскольку количество вырезаний равно , то четность количества треугольников разбиения совпадает с четностью количества сторон. Значит, на 6 треугольников семиугольник не разбить.
Можно иначе: рассмотрим четырехугольники разбиения. Они дают от двух до четырех треугольников. Причем из любой вершины многоугольника может выходить диагональ только в ту вершину , которая вместе с находится в одном из четырехугольников разбиения (иначе диагональю резался бы по двум сторонам какой-нибудь треугольник). Поэтому структура разбиения проста: несколько четырехугольников, несколько треугольников. Причем четырехугольники на четность не влияют, их можно исключить и рассматривать треугольники, все вершины которых являются вершинами многоугольника. После этого рассуждения очевидны.
1й Пусть было х блоков, тогда: х-1/2х-(1/2)(5/9)х=8; 1/2х-5/18х=8; 9/18х-5/18х=8; 4/18х=8; х=8÷4/18; х=8×18/4; х=36. 36×(1/2)=18(блоков)-1й мальчик; 18×(5/9)=10(блоков)-2й мальчик; (18+8)÷10=26÷10=2.6=2_3/5(раза)-во столько больше положили 1й и 3й малики больше блоков, чем 2й.
2й 1-1/2=1/2(блоков)-ост.после первого мальчика; 1/2 × 5/9=5/18(блоков)-использовал 2й мальчик; 1/2+5/18=9/18+5/18=14/18(блоков)-использовали 1й и 2й мальчики; 1- 14/18=18/18 - 14/18=4/18(блоков)-использовал 3й мальчик; 8÷4×18=36(блоков)-было всего. 36×(1/2)=18(блоков)-1й мальчик; 18×(5/9)=10(блоков)-2й мальчик; (18+8)÷10=26÷10=2.6=2_3/5(раза)-во столько больше положили 1й и 3й малики больше блоков, чем 2й.
1 рабочий: Пусть х-время работы( часы). Изготавливает 780 дет. Значит его скорость работы = 780\х 2 рабочий: Если у первого-х, а по условию первый рабочий тратит на 4 часа меньше, значит время= х+4. Изготавливает 840 дет. Значит его скорость работы= 840\ х+4. Разница между первой скоростью и второй составляет 2 детали в час. Составим уравнение: 780\х - 2= 840\(х+4) 780\х - 840\(х+4) - 2=0 780*(х+4)-840х - 2*(х²+4х)=0 780х+3120-840х-2х²-8х=0 -2х²-68х+3120=0 2х²+68х-3120=0 х²+34х-1560=0 D: 34²-4*(-1560)= 1156+6240=7396 √7396=86 1)х= -34-86\2= -120\2=-60 ( Не удовлетворяет условию, так как работа не может быть отрицательной) 2) х= 86-34\2=52\2=26. Теперь поу словию, нам нужно найти работу 1 рабочего=( 780\х)= 780\26=30. ответ: 30
Пример для пяти очевиден: все диагонали из одной вершины. Пример для семи: возьмем квадрат, проведя в нем все диагонали. После этого "облепим" его одинаковыми треугольниками (так, чтобы их внутренние углы были не 45 градусов) с трех сторон.
Пусть треугольников разбиения
. Будем вырезать их, но на каждом ходу будем вырезать только такой, у которого хотя бы одна сторона является стороной многоугольника. Тогда количество сторон либо увеличивается на 1, либо уменьшается на 1, либо даже уменьшается на 3. Все эти числа нечетны. Поскольку количество вырезаний равно 
, то четность количества треугольников разбиения совпадает с четностью количества сторон. Значит, на 6 треугольников семиугольник не разбить.
Можно иначе: рассмотрим четырехугольники разбиения. Они дают от двух до четырех треугольников. Причем из любой вершины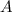
многоугольника может выходить диагональ только в ту вершину 
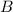, которая вместе с 
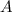находится в одном из четырехугольников разбиения (иначе диагональю резался бы по двум сторонам какой-нибудь треугольник). Поэтому структура разбиения проста: несколько четырехугольников, несколько треугольников. Причем четырехугольники на четность не влияют, их можно исключить и рассматривать треугольники, все вершины которых являются вершинами многоугольника. После этого рассуждения очевидны.