a∈(2;6)
Пошаговое объяснение:
(a+3)(a-2)<a²
a²+a-6-a²<0
a-6<0
a<6
но поскольку а-2>0;
a>2
2<a<6
 AC=8 см. В прямоугольнике противоположные стороны равны, значит AB=CD=8 см. Точка пересечения делит диагонали пополам, отсюда BO=
AC=8 см. В прямоугольнике противоположные стороны равны, значит AB=CD=8 см. Точка пересечения делит диагонали пополам, отсюда BO=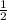 BD=8 см, AO=
BD=8 см, AO=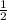 AC=8 см.
AC=8 см.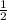 AC=8 см. В прямоугольнике противоположные стороны равны, значит AB=CD=8 см. Точка пересечения делит диагонали пополам, отсюда BO=
AC=8 см. В прямоугольнике противоположные стороны равны, значит AB=CD=8 см. Точка пересечения делит диагонали пополам, отсюда BO=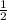 BD=8 см, AO=
BD=8 см, AO=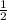 AC=8 см.
AC=8 см.
2<а<6
Пошаговое объяснение:
Дано:
Сторона квадрата - а
Длина прям. на 3см> чем а
Ширина прям. на 2см<чем а
S(квадрата)-S(прям.)= @
Найти: а
S(квадрата)=а×а=а^2 (см^2)
Длина прям. - (а+3) см
Ширина прям. - (а -2) см
S(прям.)=(а+3)(а-2)
S(квадрата)-S(прям.)=
=а^2-(а+3)(а-2)=
=а^2-(а^2-2а+3а-6)=
=а^2-а^2+2а-3а+6=
=6-а
Возможные значения а:
0<а<6
С другой стороны:
ширина прям. а-2>0
а>2
В итоге:
2<а<6