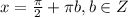![Т3) Сколько корней имеет уравнение |cosx| + корень(sin2x) =0 на отрезке [0; 2пи] Заранее большое](/tpl/images/3779/5884/461ca.jpg)
Для точного ответа недостаточно информации. Пять точек можно соединить по-разному, задействовав разное количество лучей (или отрезков).
Начнём с того, что фраза "никакие три точки не лежат на прямой" говорит нам, что любой луч будет соединять не меньше чем две (иначе он ничего не соединяет) и не больше чем две (противоречит условию) точки.
В минимальном случае достаточно n-1 = 4 луча - если условно пронумеровать точки, то лучи, пущенные между 1 и 2, 2 и 3, 3 и 4, 4 и 5 соединят все точки незамкнутой ломаной.
Если мы считаем, что лучи могут лежать на одной прямой, если выпущены из разных точек, то максимальное количество лучей равно 5 * (5-1) = 20. Это значит, что каждую из пяти точек можно соединить с четырьмя другими.
Если считаем, что лучи не могут лежать на одной прямой, то максимум их будет 5 * (5-1) / 2 = 10, потому что в предыдущем пункте лучи дублировались для каждой пары точек из первой во вторую, из второй в первую.
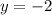 .
.
Пошаговое объяснение:
Дано уравнение: 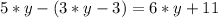
Для начала раскроем скобки в левой части уравнения, и так как перед скобкой стоит знак "-", то при раскрытии скобок, знаки в ней поменяются на противоположные:
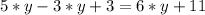
Теперь приведем подобные в левой части уравнения:
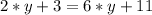
Далее неизвестные мы перебрасываем в правую часть уравнения, известные в левую. В правую сторону удобнее, чтобы знак "-" был не у неизвестной переменной, а у числа. Помним, что при переносе с одной стороны уравнения в другую, знак перед числом или переменной всегда меняется на противоположный:
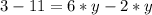
Упростим:
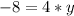
В итоге получаем что 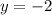 :
:
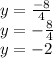 .
.
Можно решить двумя Рассмотрим первый:
Исходя из этого понимаем, что выражение равно нулю только в том случае, если оба неотрицательных слагаемых равны нулю:
ответ: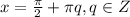
Второй
Данное уравнение равносильно следующей системе:
Так как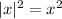 , то:
, то:
Модуль - это число неотрицательное. А это значит, что неравенство системы имеет смысл только тогда, когда cos(x) = 0:
Первое уравнение системы, очевидно, имеет решение cos(x) = 0. ответ получаем тот же.
ответ: