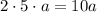
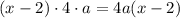
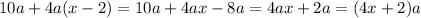
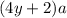 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: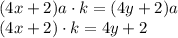
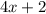 и выражение
и выражение 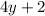 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном 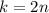 возникает противоречие:
возникает противоречие: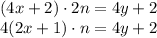
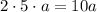
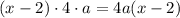
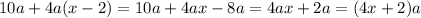
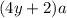 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: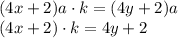
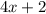 и выражение
и выражение 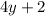 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном 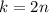 возникает противоречие:
возникает противоречие: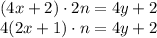
1) 5 7/9 + 5/6 - 6 1/2 = 5 14/18 + 15/18 - 6 9/18 = 5 29/18 - 6 9/18 = 6 11/18 - 6 9/18 = 2/18 = 1/9
2) 87 48/49 - 78 48/49 = 9
3) 2 5/6 * 1/9 : 1/2 * 9 = 17/6 * 1/9 * 2 * 9 = 17/54 * 18 = 17/3 = 5 2/3
2.
1) 17 : 1/5 = 17 * 5 = 85
2) 1 5/96 : 1/8 = 101/96 * 8 = 101/12 = 8 5/12
3) 2 1/2 * 1 13/45 * 4 = 5/2 * 58/45 * 4 = 29/9 * 4 = 116/9 = 12 8/9
4) 85 - 8 5/12 + 12 8/9 - 82 13/18 = 84 36/36 - 8 15/36 + 12 32/36 - 82 26/36 = 6 27/36 = 6 3/4