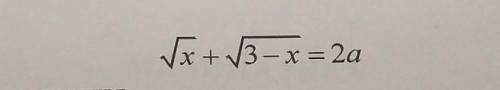
1. Пусть 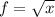 ,
, 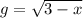 . Заметим, что
. Заметим, что 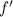 и
и 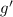 монотонно убывают, значит,
монотонно убывают, значит, 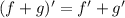 функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения
функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения 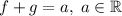 не более двух корней.
не более двух корней.
2. Заметим, что если 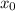 является решением, то
является решением, то  тоже. Очевидно, что
тоже. Очевидно, что 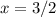 является осью симметрии (причем единственной) графика
является осью симметрии (причем единственной) графика 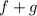 . Иначе говоря, пара
. Иначе говоря, пара 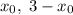 исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы
исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы 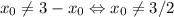 . Итак,
. Итак, 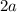 пробегает область значения рассматриваемой функции, кроме того
пробегает область значения рассматриваемой функции, кроме того  , которому соответствует
, которому соответствует 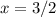 (это
(это 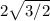 ).
).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение 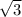 , а наибольшее в
, а наибольшее в 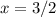 . Получаем ответ:
. Получаем ответ: 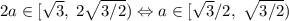

Поставь лайк и отметить как лучшее решение
а) |7х|=24,5 (вычеслить)
7×|х|= 24,5 (разделяем обе стороны)
|х|=3,5 (рассмотрим все возможные случаи)
х=3,5 х=–3,5 (уравнения имеет 2 решения)
Х1=3,5 Х2=–3,5
б) |5х+2,1|=0,2 (рассмотреть все возможные случаи)
5х+2,1=0,2
5х+2,1=–0,2 (решить уравнения)
х=–0,38
х=–0,46 (уравнения имеет 2 решения)
Х1=–0,38 Х2=–0,46
с) |9х+27|-4=0,5 (перенести константу в правую часть уравнения)
|9х+27|=0,5+4 (вычислить)
|9х+27|=4,5 (рассмотреть все возможные случаи)
9х+27=4,5
9х+27=–4,5 (решить уравнения)
х=–2,5
х=–3,5 (уравнения имеет 2 решения)
Х1=–3,5 Х2=–2,5
Поставь лайк и отметить как лучшее решение
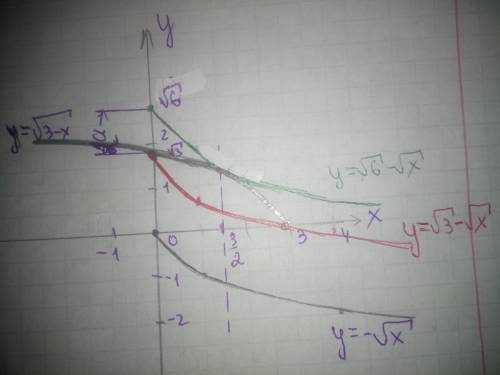
Графический решения.